Основой изучения личного потребления (индивидуальных потребителей и домашних хозяйств) служат кривые безразличия. Кривая безразличия – линия, каждая точка которой представляет собой такую комбинацию двух товаров, что потребителю безразлично, которую из них выбрать. Кривые безразличия графически отражают систему предпочтений потребителя.
Для удобства воспроизведения используется двумерное пространство, т.к. выводы, полученные для двумерного случая (для двух товаров), справедливы для сколь угодно большого количества товаров.
Рассмотрим простой пример. Допустим, домашнее хозяйство может потреблять два вида благ (благо 1 и благо 2). Пусть в течение некоторого периода первое благо потребляется в количестве y1, а второе – в количестве Y2. Двумерный вектор (y1, y2) назовем планом потребления. Домашнее хозяйство сравнивает вектор потребления (набор потребляемых благ) А= (Y1A, Y2A) с другим вектором потребления, В = (Y1B, Y2B) и выносит одно из следующих суждений:
а) вектор А предпочтительнее, чем вектор В;
б) вектор В предпочтительнее, чем вектор А;
в) векторы А и В равно предпочтительны (потребителю безразлично, какой из векторов А или В выбрать).
Кривая безразличия здесь – это все планы потребления, которые находятся в отношениях безразличия с рассматриваемым планом потребления.
Если обозначить через U = U(y1, y2) функцию, или, иначе говоря, индекс полезности, которую можно получить от потребления благ, заданных вектором (y1, y2), то кривая безразличия это набор значений
(y1, y2), которые приводят к одному и тому же значению U.
Существуют различные виды кривых безразличия, определяемые способом задания функции полезности. Но существуют также и общие свойства кривой безразличия, независимо от её вида:
через любую точку в графическом пространстве товаров всегда можно провести соответствующую кривую безразличия, т.к. для любой комбинации двух товаров всегда найдётся множество других комбинаций, полезность которых будет такой же, как у этой точки. Данное свойство основано на том, что потребитель может сравнить все товары или их набор с помощью отношений предпочтения или безразличия (аксиома полной упорядоченности); кривые безразличия никогда не пересекаются (аксиома транзитивности и аксиома ненасыщения); на основании первых двух свойств можно построить карту кривых безразличия, содержащую информацию о системе предпочтений потребителя. Кривая, более отдалённая от начала координат, имеет большую общую полезность: более предпочтительна; кривая безразличия имеет отрицательный наклон, так как сокращение количества одного товара должно быть компенсировано или заменено увеличением количества другого товара, чтобы была сохранена общая полезность набора; кривая безразличия в широком смысле вогнута по отношению к началу координат: наклон кривой безразличия уменьшается при движении вдоль горизонтальной оси от начала координат. Это объясняется тем, что готовность потребителя замещать один товар другим при этом падает.
Чтобы построить кривую безразличия, необходимо выразить один из аргументов функции полезности через другой аргумент и значение функции полезности U. Так, для функции полезности (1) получаем:
,
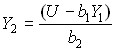а для функции (2) – получаем:
.
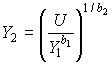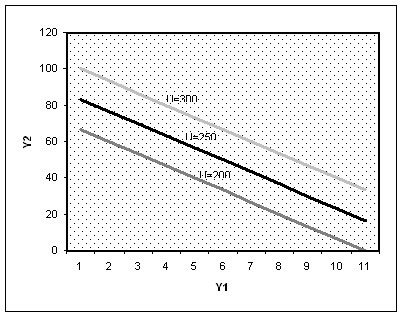
Рис. 5.7. Кривые безразличия
Данный тип кривой (Рис. 5.7.) присущ товарам-субститутам, причём, абсолютным. Это значит, что увеличение спроса на одно из двух благ (товаров) сопровождается падением спроса на другое благо: эти два блага находятся в отношениях взаимозаменяемости. В качестве примера можно привести кофе и чай.
Касательно последнего свойства кривой безразличия – при замене строгого неравенства на нестрогое в условии вогнутости функции приходим к понятию вогнутой линейной функции.
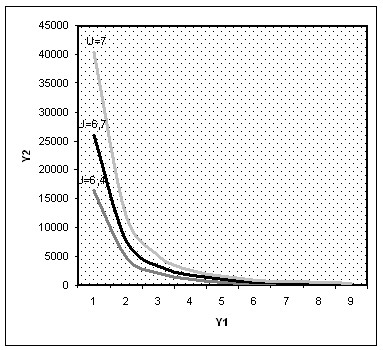
Рис.5.8. Кривые безразличия
Тип этих кривых (Рис. 5.8.), строго говоря, является одним из смешанных, так как существует ещё тип кривых безразличия для комплементарных товаров (благ). При увеличении спроса на одно из двух таких благ растет спрос и на второе благо: они находятся в отношениях взаимодополнения. Например, кофе и сахар.
Рассмотрим наборы только из двух товаров Χ и Υ. (Товары Χ и Υ можно рассматривать как комбинированные товары).
Отношения предпочтения, характерные для каждого индивида, отражают посредством кривой безразличия (рис.5.9.).
Кривая безразличия отражает множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Наборы А и В с точки зрения данного потребления равноценны и лежат на одной и той же кривой безразличия. Для нашего потребителя любой набор, лежащий на кривой II, предпочтительнее любого набора, лежащего на кривой I и т.д.
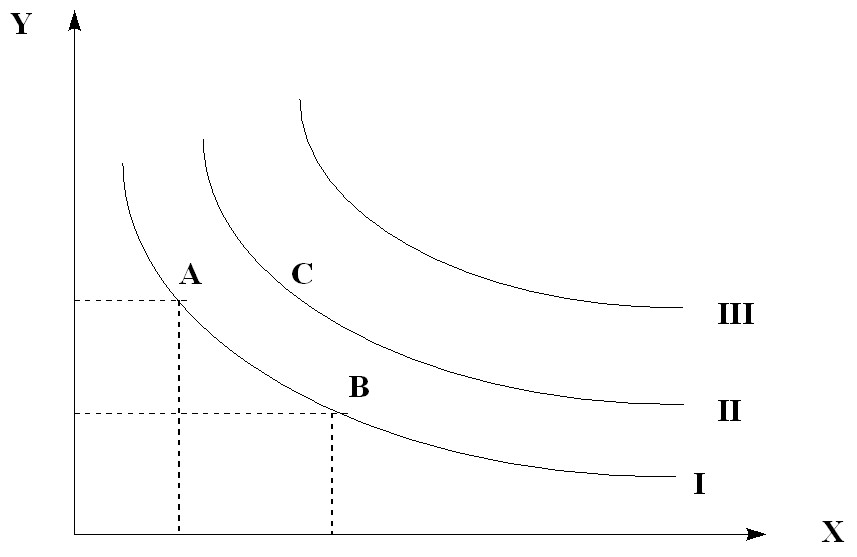
Рис. 5.9. Кривые безразличия
В зависимости от функций полезности различают следующие типы кривых безразличия:
1). Функция полезности с полным взаимозамещением благ (чай и кофе) имеет вид:
,
где a,b – параметры;
U – полезность;
X,Y – товары.
Из функции полезности можно найти Y :
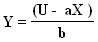
и построить кривые безразличия линейного типа (рис. 5.10.).
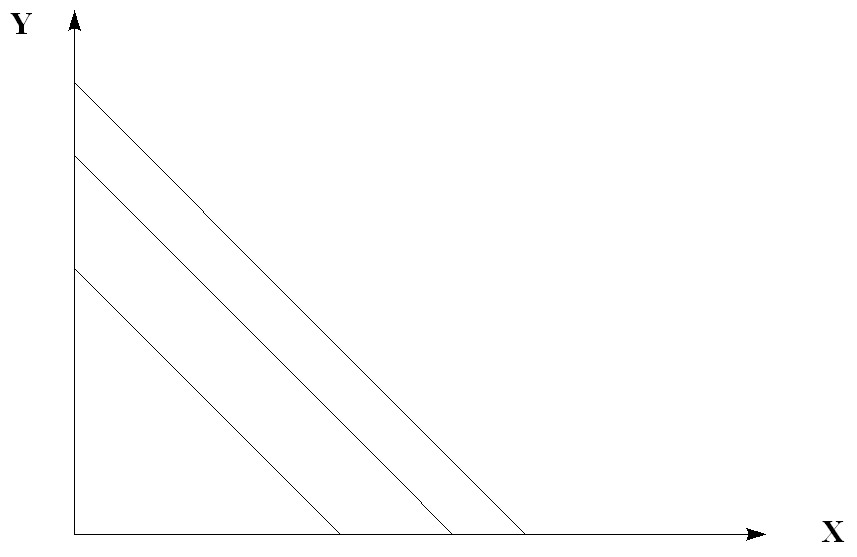
Рис. 5.10. Кривые безразличия линейного типа
2).Неоклассическая функция полезности имеет вид:
, где a+b ≤ 1
Чтобы построить кривые безразличия необходимо найти Y:
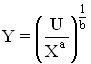
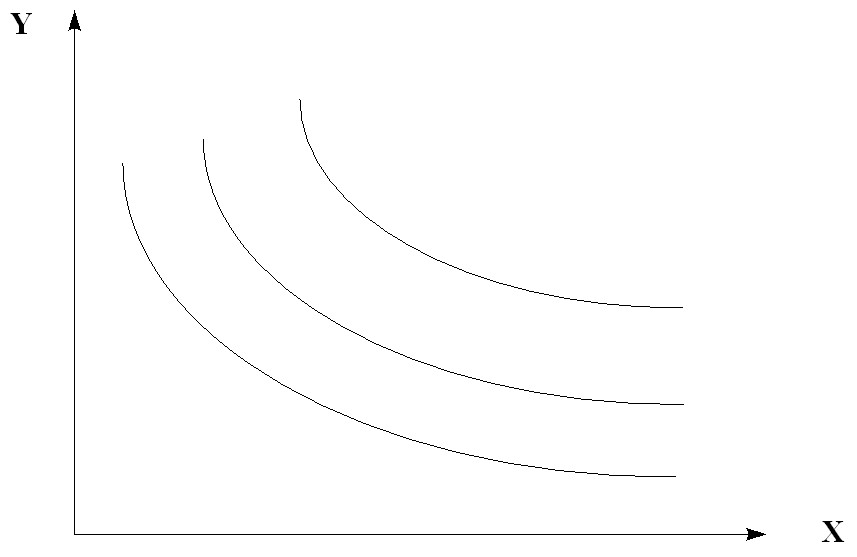
Рис. 5.11. Кривые безразличия неоклассического типа
3) Функции с полным взаимодополнением благ (при увеличении спроса на одно из двух благ растет спрос и на второе благо, например, сахар и чай, бензин и моторное масло) имеют кривые безразличия в виде точки на пересечении двух прямых. Избыток одного блага не имеет значения. Полезность достигается лишь при определенной комбинации обеих благ.
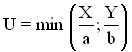
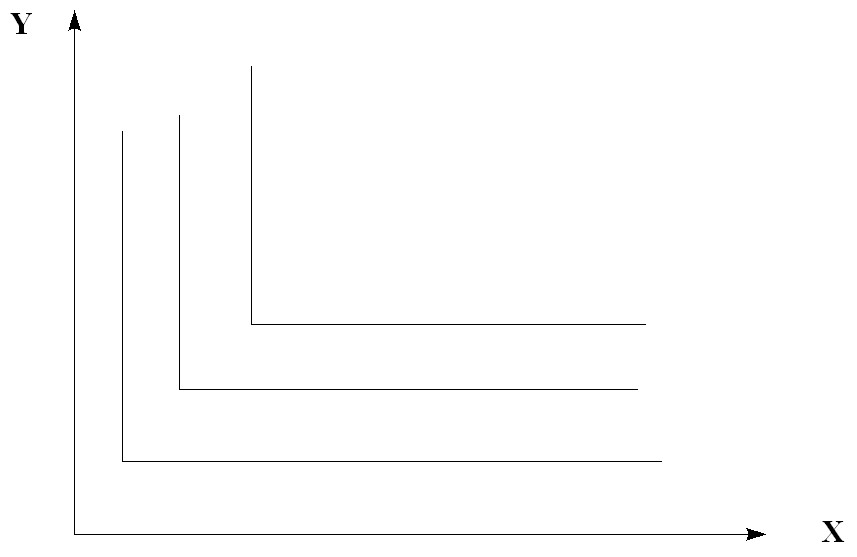
Рис. 5.12. Кривые безразличия функций с полным взаимодополнением благ
Основными понятиями теории потребления являются предельная полезность и предельная норма замещения. Пусть U(Y1, Y2) —функция полезности. Достигаемый при фиксированном уровне потребления первого блага и незначительном изменении уровня потребления второго блага прирост функции полезности называется предельной полезностью (marginal utility) второго блага. То есть предельная полезность – полезность, получаемая от потребления дополнительной единицы блага.
Величина, определяющая наклон кривой безразличия, называется предельной нормой замещения (marginal rate of substitution; MRS) потребительских благ. Она показывает, в какой степени потребитель готов заменить один товар другим, чтобы получить при этом ту же общую полезность.
Другими словами, предельной нормой замещения блага X блага Y (MRSxy) называют количество блага Y, которое должно быть сокращено «в обмен» на увеличение количества блага X на единицу, с тем чтобы уровень удовлетворения потребителя остался неизменным:
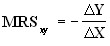при условии, что U= const
Согласно аксиоме ненасыщения, любая точка, лежащая выше кривой безразличия, всегда более предпочтительна для потребителя, обладая большей общей полезностью. А любая точка, лежащая ниже, кривой безразличия, соответственно, менее предпочтительна для потребителя.
Если использовать функцию полезности неоклассического типа, то можно убедиться в существовании закона убывающей предельной нормы замещения. Этот закон явился результатом интерпретации закона убывающей предельной полезности с позиций теории выбора (теории порядковой полезности, ординалистского подхода) и считается одной из центральных идей современной микроэкономической теории. Закон убывающей предельной нормы замещения может быть сформулирован следующим образом: при стремлении поддерживать неизменным уровень полезности путем замещения первого блага вторым субъективное удовлетворение, получаемое от предельного потребления первого блага, в сравнении с удовлетворением, получаемым от предельного потребления второго блага, будет неуклонно уменьшаться.
Естественно потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Однако, это не всегда возможно, т.к. потребительское поведение ограничивается средствами, которыми он располагает.
Если обозначать рыночные цены блага X через Рх , а блага Y через Py ,
а его доход через I, то бюджетное ограничение потребителя можно записать в виде уравнения:
.
Доход потребителя равен сумме его расходов на покупку товаров X и Y.
Преобразуем уравнение и получим уравнение бюджетной линии, которая имеет вид прямой линии (рис. 5.13.). Чем выше доход, тем дальше от начала координат находится линия бюджетного ограничения.
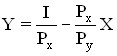
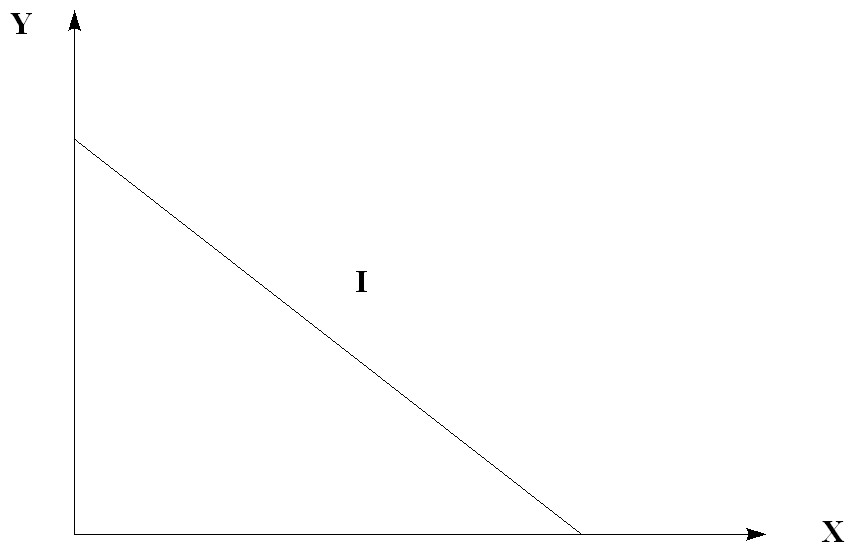
Рис. 5.13. Бюджетная линия
Пусть задана линия бюджетного ограничения и несколько кривых безразличия. Какой товарный набор выбирает потребитель?
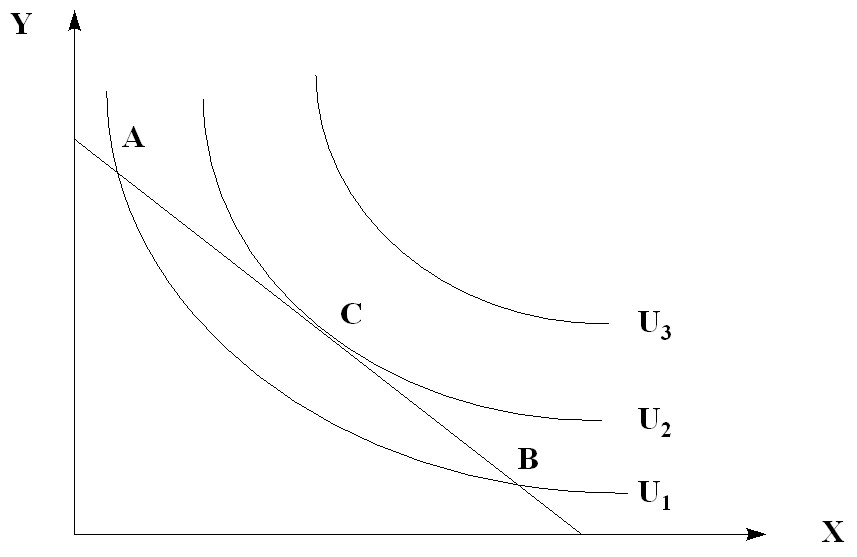
Рис. 5.14. Оптимальный выбор потребителя
Оптимум потребителя будет в точке С. В рамках бюджетного ограничения индивид постарается так распределить свой доход между различными благами, чтобы максимизировать полезность U. Соответствующий набор благ называется оптимальным планом потребления и обычно обозначается точкой касания бюджетной линии и кривой безразличия. Итак, в условиях, когда рыночные цены и доход индивида заданы извне, оптимальный план потребления индивида определяется на основе принципа максимизации полезности. Оптимальный план потребления изменяется в зависимости от цен и дохода (рис. 5.14.).
В точке оптимума выполняется равенство:
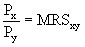
Соотношение цены блага X к цене блага Y равно предельной норме замещения блага X блага Y.
В общем случае рассмотрим потребителя (группу семей) с определенным доходом I, предназначенным для приобретения набора товаров X=(x1 ,…, xj ,…, xn), цены которых соответственно равны P=(p1 ,…, pj ,…, pn).
Здесь X,P – неотрицательные векторы.
Ограниченность возможного выбора потребителя выражается с помощью бюджетного ограничения
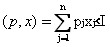
Постановка задачи оптимального выбора потребителя может быть сформулирована двояко: а) в терминах отношения предпочтения: наилучшим (оптимальным) считается набор 
, который является «наиболее предпочтительным по отношению «=
« среди всех неотрицательных векторов x, удовлетворяющих бюджетному ограничению. Наиболее предпочтительным на множестве R обычно называется набор
, обладающий тем свойством, что он удовлетворяет условию
«
=
x» для всех x ∈ R
Очевидно, что единственность такого набора, вообще говоря, не обеспечена,
б) в терминах функции полезности: оптимальный набор 
соответствует наибольшему значению u(x) в указанных выше условиях, т.е. является решением задачи:
u(x) = u(x1 ,…, xj ,…, xn) → max
при условиях
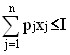; xj ≥ 0 (j = 1, … , n)
При анализе задачи оптимального выбора обычно применяется еще одно важное предположение теории потребления, которое носит название гипотезы ненасыщения потребителя и состоит в том, что для любых двух наборов x и y справедливо соотношение:
если x ≥ y, то «x =
y».
Также считается справедливым и более точное соотношение:
если x ≥ y и x ≠ y, то «x > y».
Это означает, что для «ненасыщаемого» потребителя всякий набор x, который содержит любого продукта столько же, либо (хотя бы по одной позиции) несколько больше, чем набор y, оказывается более предпочтительным. Предположение о ненасыщении при помощи функции полезности выражается следующим образом:
если x ≥ y, то u(x) ≥ u(y). если x ≥ y и x ≠ y, то u(x) > u(y).
Таким образом, функция полезности является монотонно возрастающей по каждому аргументу xj.
Если функция полезности имеет производные по своим аргументам, то из предположения о ненасыщаемости (и монотонности u(x)) следует, что все первые частные производные функции полезности являются положительными, т.е.:
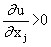(j = 1, …, n)
для любого набора потребительских благ. Величина частной производной:
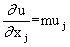
имеет следующий экономический смысл: она показывает, на сколько увеличится полезность набора, если количество потребляемого блага увеличится на «малую единицу». В связи с этим указанная производная носит название предельной (маргинальной, дифференциальной) полезности.
В экономических исследованиях, как правило, используются некоторые конкретные виды выпуклых функций полезности, причем подбор вида функции и оценка числовых значений параметров производится на основе наблюдений и анализа поведения потребителей. Чаще всего применяются линейная, квадратическая и логарифмическая функция вида:
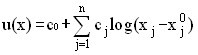
В пространстве двухэлементных наборов x=(x1, x2) поверхности безразличия (т.е. линии u(x1, x2)=const) обычно называются кривыми безразличия.
Например, для логарифмической функции:
u(x1, x2)= log x1 + log x2
кривые безразличия имеют вид:
log x1 + log x2 = log (x1 x2) = const ,
т.е. являются просто гиперболами в положительном ортанте, удовлетворяющими уравнениям:
(x1 ⋅ x2) = const
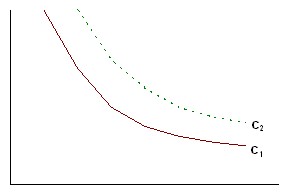
Рис. 5.15. Кривые безразличия
На рис. 5.15 C2 > C1, т.е. более высокая кривая безразличия соответствует большему уровню полезности тех наборов, которые составляют кривую безразличия.
Рассмотрим задачу оптимального выбора потребителя для ненасыщаемого потребителя:
Нетрудно заметить, что оптимальный набор 
(
,
, 
) необходимо должен удовлетворять бюджетному ограничению как точному равенству. В самом деле, если бы оптимальный набор достигался бы при условии:
,
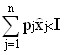то потребитель мог бы купить на оставшиеся деньги некоторое количество любого блага, и тем самым получить новый набор с большей полезностью. Это означает, что внутренняя точка множества не может быть оптимальным набором.
Таким образом, задача об оптимальном наборе имеет вид:
u(x) = u(x1 ,…, xj ,…, xn) → max
.
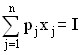Решение этой задачи на условный экстремум находится при помощи метода множителей. Оптимальный набор определяется путем решения следующей системы из (n+1) уравнения:
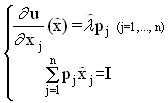
относительно (n+1)-го неизвестного, а именно элементов оптимального набора (
,
, 
) и множителя Лагранжа 
.
Таким образом, при заданной системе цен потребитель должен выбрать такой набор, а котором все предельные полезности пропорциональны ценам. При этом оптимальное значение множителя Лагранжа 
часто называют «предельной полезностью денег» и трактуют как прирост максимальной полезности при увеличении дохода I на малую единицу. Заметим, что соотношения оптимальности могут быть представлены в виде:
,
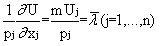который допускает любопытную интерпретацию: в оптимальной точке величина дополнительной полезности в расчете на одну денежную единицу должна быть одинакова для всех товаров и услуг. Необходимо также отметить, что для некоторых товаров могут быть выполнены соотношения:
,
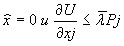которые означают, что такие товары сравнительно мало полезны и относительно дороги, а поэтому и не должны быть включены в оптимальный набор потребителя, максимизирующего свою полезность при ограниченном доходе.
Рассмотрим простой пример.
Пусть n=2, функция полезности:
u(x1, x2) = ln x1 + ln x2,
бюджетное ограничение:
p1x1 + p2x2 = I.
Решение задачи оптимального выбора
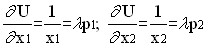
отсюда:
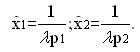
Используя бюджетное ограничение, имеем:
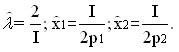
Как видно из приведенного решения оптимальный выбор потребителя имеет очень естественный вид: количество потребляемого блага прямо пропорционально доходу (I) и обратно пропорционально его цене. Геометрическая интерпретация решения задачи оптимального выбора приведена на рис. 5.14.
В более реалистичных вариантах постановки задачи оптимального выбора при помощи дополнительных условий могут быть учтены ограничения по ассортименту потребляемых товаров и услуг, возможность взаимной замены различных продуктов и т.п.