Средней величиной называется обобщающая характеристика совокупности однотипных общественных явлений по одному количественному признаку в определенных условиях места и времени.
При вычислении средних обобщающих показателей выявляются общие для данной совокупности типические размеры уровня того или иного признака и тем самым выявляются общие для нее типические черты и свойства.
Метод средних величин представляет собой особую форму статистического обобщения. Применение метода средних величин возможно только при наличии вариации признака у совокупности однородных явлений.
Средние величины могут быть как абсолютными, так и относительными (средняя заработная плата, средний процент выполнения плана).
Уровень признака у отдельных единиц совокупности складывается под влиянием разнообразных условий, одни из них являются общими для всех единиц, другие – случайными. В средней величине, исчисленной на основе данных о большом числе единиц, колебания в величине признака, вызванные случайными причинами, погашаются, и проявляется общее свойство для всей совокупности. При осреднении все отклонения признака от среднего уровня уравновесились, т.е. произошло отвлечение (абстрагирование) от индивидуальных особенностей отдельных единиц, т.е. средняя величина абстрактна, и в этом заключается ее научная ценность.
Средняя величина правильно характеризует однородные по своему содержанию совокупности. Такая средняя будет типичной, так как она отражает то общее, что характерно для данной совокупности общественных явлений.
Если же совокупность в целом по составу неоднородна, то для получения типичных средних необходимо с помощью метода группировок расчленить такую совокупность на однородные группы и после этого исчислить средние величины для каждой группы отдельно.
Средняя величина всегда именованная, она имеет ту же размерность, что и признак у отдельных единиц совокупности.
Объективность и типичность статистической средней могут быть обеспечены лишь при определенных условиях. Первое условие состоит в том, что средняя должна вычисляться для качественно однородной совокупности. Второе условие – для исчисления средней должны быть использованы не единичные, а массовые данные, ибо только тогда взаимо погашаются возможные случайные отклонения.
Следует помнить о том, что чрезмерное увлечение средними показателями может привести к необъективным выводам при проведении анализа. Это связано с тем, что средние величины, будучи обобщающими показателями, погашают, игнорируют те различия в количественных признаках отдельных единиц совокупности, которые реально существуют и могут представлять самостоятельный интерес.
В статистике применяется несколько видов средних величин:
средняя арифметическая; средняя гармоническая; средняя квадратическая; средняя геометрическая; средняя хронологическая.
Эти средние относятся к классу степенных средних. Кроме них используются структурные средние – мода и медиана.
Средняя арифметическая – основной вид средних величин. Она может быть простой и взвешенной.
Средняя арифметическая простая исчисляется путем деления суммы значений признака на число значений:
,
где 
— средняя арифметическая;
— отдельные значения признака;
— число значений признака.
Пример.
По состоянию на 14 октября имеются следующие данные о расходе металла 8 рабочими (кг): 17,2; 19,0; 20,0; 17,0; 18,0; 19,8; 18,0; 18,6 Для того чтобы определить средний расход металла на одного рабочего, необходимо общий расход металла разделить на число рабочих:
кг.
Если данные представлены в виде дискретного ряда распределения, то расчет средней производится по формуле средней арифметической взвешенной:
,
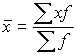где х – значение признака;
f – частота повторения соответствующего признака (веса).
Пример.
Таблица 12
Затраты времени на обработку детали
Затраты времени (сек) на обработку детали (х) | 46 | 48 | 50 |
Число деталей (f) | 250 | 400 | 150 |
Определить средние затраты времени на обработку детали:
.
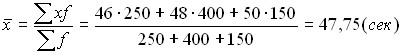Если данные представлены в виде интервального ряда распределения, то принцип расчета средней остается прежним, но предварительно вычисляется среднее значение признака для каждого интервала, представляющее полусумму нижнего и верхнего значений интервала:
,
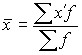где: 
;
— нижняя граница интервала;
— верхняя граница интервала.
Если есть интервалы с открытыми границами, то для первой группы величина интервала берется равной величине интервала последующей группы.
Пример.
Таблица 13
Стаж работы рабочих цеха
Стаж работы, лет (х) | до 6 | 6-12 | свыше 12 |
Число рабочих (f) | 15 | 25 | 10 |
Определить средний стаж рабочих цеха.
Он равен:
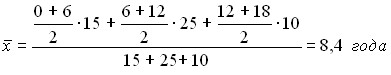
Средняя гармоническая представляет собой обратную величину средней арифметической из обратных величин. Она бывает простая и взвешенная:
простая –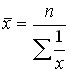 
; взвешенная – 
.
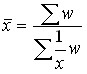Средняя квадратическая используется в том случае, когда необходимо возводить варианты в квадрат:
простая –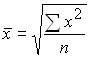 
; взвешенная – 
.
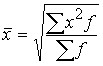Средняя квадратическая применяется в технике, для расчета среднего квадратического отклонения.
Средняя геометрическая – 
.
Средняя хронологическая:
простая –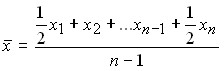 
;
(Она применяется в том случае, когда интервалы времени между явлениями равны).
взвешенная –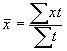 
;
(Она применяется в том случае, когда интервалы времени между явлениями неравны).
Свойства средней арифметической.
1. Средняя арифметическая из постоянных чисел равна этому постоянному числу.
Пусть х = a, тогда: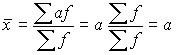 
.
2. Если веса всех вариантов пропорционально изменить, т.е. увеличить или уменьшить в одно и то же число раз, то средняя арифметическая нового ряда от этого не изменится. Пусть f уменьшим в к раз. Тогда:
.
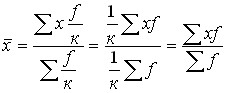3. Если все варианты уменьшить или увеличить на какое-либо число, то средняя арифметическая нового ряда уменьшится или увеличится на столько же.
Уменьшим все варианты х на а, т.е. 
. Тогда:
.
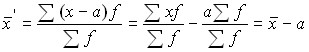Среднюю арифметическую первоначального ряда можно получить, прибавляя к средней арифметической нового ряда, ранее вычтенное из вариантов число a, т.е. 
.
4. Если все варианты уменьшить в к раз, то средняя арифметическая нового ряда уменьшится в к раз.
Пусть 
, тогда 
.
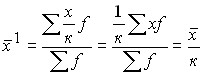Среднюю арифметическую первоначального ряда можно получить, увеличив среднюю арифметическую нового ряда в 
раз: 
.
5. Сумма положительных и отрицательных отклонений отдельных вариантов от средней, умноженных на веса, равна нулю.
.
Перечисленные свойства позволяют в случае необходимости упрощать расчеты путем замены абсолютных частот относительными, уменьшать варианты на какое-либо число а, сокращать их в к раз и рассчитывать среднюю арифметическую из уменьшенных вариантов, а затем переходить к средней первоначального ряда. Способ исчисления средней арифметической с использованием ее свойств известен в статистике как способ «условного нуля» или «условной средней», а также как «способ моментов».
Этот способ расчета находит отражение в следующей формуле: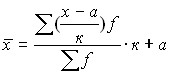 
.
Если уменьшенные варианты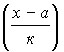 
обозначить через
, то 
.
Для характеристики среднего значения признака в вариационном ряду используется средняя арифметическая, мода и медиана.
Мода – это наиболее часто встречающееся значение признака в совокупности. Медианой называется численное значение признака, расположенное в середине ранжированного ряда, которое делит этот ряд на две равные по численности части. Для определения медианы сначала находят ее место в ряду по формуле 
, где n – число членов ряда (
). Если число единиц четное, то место медианы в ряду определяется как 
.
Применяется мода при экспертных оценках, при установлении размера изделий, который пользуется наибольшим спросом (одежда, обувь), медиана используется при статистическом контроле качества продукции.
Пример.
Таблица 14
Распределение рабочих цеха по квалификации
тарифный разряд (х) | II | III | IV | V | VI |
число рабочих (f) | 10 | 22 | 48 | 55 | 20 |
накопленные частоты (F) | 10 | 32 | 80 | 135 | 155 |
Модальным является V разряд, так как он обладает наибольшей частотой (
).
Место медианы в ряду: 
.
Медианным является IV разряд. Для определения медианы использовали накопленные частоты, которые получают последовательным суммированием частот. Накопленная частота для II разряда равна его частоте, для III разряда – это сумма частоты III разряда и накопленной частоте II разряда, то есть 22 + 10 = 32 и т.д.
При исчислении моды и медианы в интервальном ряду необходимо сначала определить интервал, в котором они находятся, среднее значение этого интервала соответствует их приближенному значению.
Пример.
Таблица 15
Распределение автомобилей по величине суточного пробега
Суточный пробег (х) | 90-130 | 130-160 | 160-190 | 190-230 | 230-270 |
Число автомобилей (f) | 70 | 160 | 130 | 85 | 20 |
Накопленные частоты (F) | 70 | 230 | 360 | 445 | 465 |
Модальным является интервал [130 – 160], среднее значение которого 145 км; Мо = 145 км.
Место медианы 
член. По накопленным частотам определяем медианный интервал [160 – 190] [Ме = 175 км].
Для определения моды в рядах с равными интервалами распределения модальный интервал определяется по наибольшей частоте, а в рядах с неравными интервалами – по наибольшей плотности распределения.
Для определения моды в рядах с равными интервалами используют формулу:
,
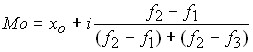где 
— нижняя граница модального интервала;
— величина интервала;
— частоты предмодального, модального и послемодального интервала.
Моду можно определить графически по гистограмме. Для этого в самом высоком столбце гистограммы от границ 2-х смежных столбцов проводят линии, затем из точки их пересечения опускают перпендикуляр на ось абсцисс. Значение признака на оси абсцисс и будет соответствовать моде.
Для расчета медианы в интервальном ряду воспользуемся следующими формулами:
,
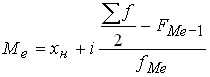или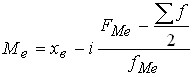 
,
где:
— нижняя граница медианного интервала; i –величина интервала медианного;
— порядковый номер медианы;
— частота, накопленная до медианного интервала;
— частота медианного интервала.
— верхняя граница медианного интервала;
— накопленная частота медианного интервала.
Медиану можно определить графически. Для этого строится кумулята. Для определения Ме высоту наибольшей ординаты делят пополам. Через полученную точку проводятся прямую, параллельную оси абсцисс до пересечения ее с кумулятой. Абсцисса точки пересечения и является Ме.
Наряду с медианой для более полной характеристики совокупности применяют и другие значения вариантов, занимающих в ранжированном ряду вполне определенное положение. К ним относят квартили и децили.
Квартили делят ряд по сумме частот на 4 равные части, а децили на 10 равных частей. Квартилей насчитывается три, а децилей — девять.
Расчет этих показателей вариационном ряду аналогичен расчету медианы. Он начинается с нахождения порядкового номера соответствующего варианта и определения по накопленным частотам того интервала, в котором этот вариант находится. Формулы для квартилей в интервальном вариационном ряду имеют следующий вид:
нижний (или первый квартиль)
,
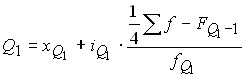верхний (или третий квартиль)
,
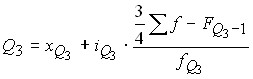где:
— нижние границы соответствующих квартильных интервалов;
– величина соответствующего интервала;
– сумма частот ряда;
– накопленные частоты интервалов, предшествующие соответствующим квартильным;
— частоты соответствующих квартильным интервалов.
Вторым квартилем является медиана.
По соотношению между средней арифметической, модой и медианой можно судить о характере распределения. В симметричных распределениях все три показателя совпадают. Чем больше расхождение между модой и средней арифметической, тем больше асимметричен ряд.
Эмпирически установлено, что для умеренно асимметричных рядов разность между модой и средней арифметической примерно в 3 раза превышает разность между медианой и средней 
. Это соотношение можно использовать в отдельных случаях для определения третьего показателя по двум известным.
Контрольные вопросы
Что называется средней величиной в статистике? Способы определения средней арифметической величины. Основные свойства средней арифметической. Что такое мода и способы ее расчета. Что такое медиана и способы ее расчета.