Межотраслевой анализ базируется на использовании статистических таблиц, называемых «межотраслевыми». Таблица межотраслевого баланса описывает потоки товаров и услуг между всеми секторами народного хозяйства в течение фиксированного периода времени (как правило, 1 год). Таблицу межотраслевого баланса, выраженную в стоимостных показателях, можно интерпретировать как систему национальных счетов. Вы можете легко представить себе структуру такого рода таблиц, взглянув на пример.
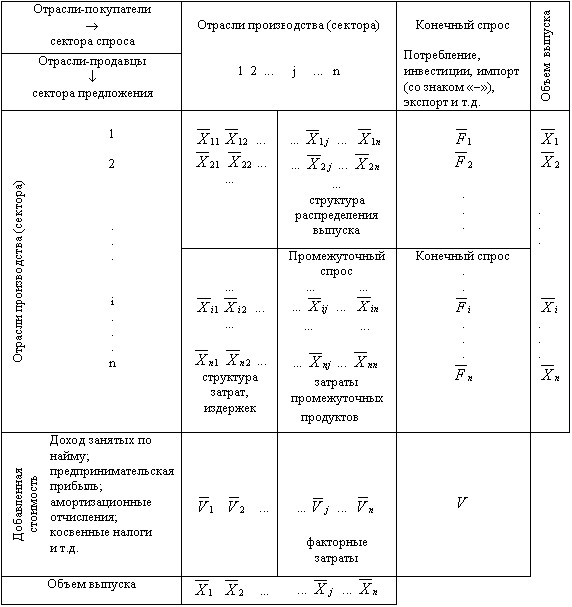
В межотраслевом балансе для страны или региона, осуществляющих торговлю с зарубежными странами, экспорт может быть представлен положительными, а импорт отрицательными – компонентами конечного спроса.
Строки приведенной таблицы показывают распределение выпуска (output) каждого вида продукции. Каждая строка характеризуется следующим балансом:
Выпуск данного вида продукции = Промежуточный спрос + Конечный спрос
что математически может быть записано как:
| (9-1) |
Промежуточный спрос есть часть общего спроса, представляющая собой закупки данного вида продукции отраслями 1, 2, 3 и так далее в качестве исходных материалов, т.е. в качестве промежуточных продуктов. Напротив, конечный спрос – это продукт, направленный в область конечного использования, т.е. он распределяется в непромышленные секторы экономики. Сюда включается личное потребление населения, расходы на содержание государственного аппарата, просвещение, здравоохранение и так далее.
Столбцы таблицы показывают структуру затрат (input) или структуру используемых ресурсов, необходимых для каждой отрасли. Для столбцов устанавливается следующий баланс:
Расходы отрасли = Промежуточные затраты + Добавленная стоимость,
что в математической записи выглядит так:
| (9-2) |
Промежуточные затраты представляют собой исходные материалы, закупленные отраслью у секторов 1, 2, 3 и так далее. Добавленная стоимость есть факторные затраты отрасли, то есть вновь созданная стоимость, распадающаяся на доход работающих по найму (заработную плату) и предпринимательский доход (прибыль).
Для строк и столбцов таблицы межотраслевого баланса имеют место следующие тождества:
Выпуск отрасли = Расходы отрасли
Общая сумма конечного спроса = Общая сумма добавленной стоимости,
которые математически записываются так:
| (9-3) |
| (9-4) |
Теперь рассмотрим схему баланса с точки зрения его крупных составных частей. Выделяют несколько блоков с различным экономическим содержанием – квадранты баланса.
В первом квадранте:
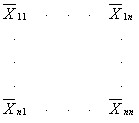
содержатся межотраслевые потоки средств производства (промежуточные затраты, производственный сектор). По форме это квадратная матрица. Данные этого квадранта играют решающую роль в анализе структуры материальных затрат отраслей, пропорций и производственных связей между отраслями, потоков в системе материального снабжения.
Во втором квадранте:
![]()
представлена конечная продукция всех отраслей материального производства. В развернутой схеме баланса конечная продукция каждой отрасли показана дифференцировано по направлениям использования: на личное потребление населения, общественное потребление (органы управления, просвещения, науки и так далее), на накопление и другое. Второй квадрант характеризует отраслевую материальную структуру национального дохода, его распределение на фонд накопления и фонд потребления.
Третий квадрант:
![]()
также характеризует национальный доход, но со стороны его стоимостного состава. Элементы третьего квадранта – это стоимостный эквивалент конечного продукта, в зарубежной литературе эти элементы называют первичными затратами. В развернутой схеме баланса этот квадрант содержит различные виды доходов работников материального производства. Данные третьего квадранта необходимы для анализа соотношений между вновь созданной и перенесенной стоимостью, между величиной необходимого и прибавочного продукта в целом по материальному производству и в отраслевом разрезе.
Отметим, что общие итоги второго и третьего квадранта равны:
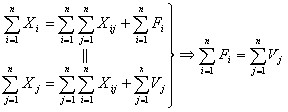
Таким образом, в межотраслевом балансе соблюдается важнейший принцип единства материально-вещественного и стоимостного состава национального дохода.
Четвертый квадрант:
![]()
отражает конечное распределение и использование национального дохода. В результате перераспределения первично созданного национального дохода образуются конечные доходы населения, предприятий, государства. Их величиной определяется доля участия населения, государственных и иных предприятий и учреждений в потреблении и накоплении всей массы конечной продукции. Данные этого квадранта важны для отражения в межотраслевой модели баланса доходов и расходов населения, источников финансирования капиталовложений, для анализа общей структуры конечных доходов по группам потребителей.
В целом межотраслевой баланс в рамках единой экономико-математической модели объединяет балансы отраслей материального производства, баланс всего общественного продукта, балансы национального дохода, финансирование доходов и расходов населения.
Наряду с межотраслевым балансом в стоимостном исчислении, как уже отмечалось, разрабатываются межпродуктовые балансы в натуральном выражении. Натуральный баланс содержит перечень не отраслей, а самих продуктов материального производства: уголь, нефть, чугун, сталь и тому подобное. В качестве единиц измерения выступают специфические для каждого продукта количественные характеристики: вес, объем, площадь, длина, киловатт-часы и другие.
Таблица межотраслевого баланса на национальном уровне составляется в настоящее время приблизительно в восьмидесяти странах. Также составляется много межотраслевых балансов на уровне регионов и крупных городов. Число секторов, которые описывают экономическую систему, в последнее время значительно увеличилось. Некоторые из наиболее детализированных таблиц описывают национальную экономику в разрезе 500-600 отдельных секторов.
Таблица межотраслевого баланса позволяет изучать структуру потоков ресурсов, однако для понимания функционирования экономики, в частности эффекта распространения (мультипликации), мы должны сделать ещё один шаг, заключающийся в построении таблиц коэффициентов прямых затрат и коэффициентов полных затрат.
Коэффициент прямых затрат определяется как объём ресурса i, необходимый для производства единицы продута j, т.е.
| (9-5) |
Множество коэффициентов затрат всех секторов рассматриваемой экономики, представленных в форме прямоугольной таблицы, соответствующее таблице межотраслевого баланса для той же самой экономики, называется структурной матрицей этой экономики. На практике структурные матрицы обычно вычисляются на основе межотраслевого баланса в стоимостном выражении.
После подстановки Xij = aijXj в (7-1) получаем:
| (9-6) |
что вплотную подводит нас к центральному вопросу межотраслевого анализа – как изменится объём выпуска отрасли Xi, если при фиксированном коэффициенте прямых затрат aij значение ![]() изменится на
изменится на ![]() Fi , т.е. Fi =
Fi , т.е. Fi = ![]() +
+ ![]() Fi. Иными словами, для каждой отрасли допускается существование производственной функции с неизменным эффектом масштаба (затраты прямо пропорциональны выпуску) и с отсутствием взаимозаменяемости ресурсов (соотношение затрат фиксировано и не зависит от уровня выпуска).
Fi. Иными словами, для каждой отрасли допускается существование производственной функции с неизменным эффектом масштаба (затраты прямо пропорциональны выпуску) и с отсутствием взаимозаменяемости ресурсов (соотношение затрат фиксировано и не зависит от уровня выпуска).
Производственные функции могут быть записаны следующим образом:
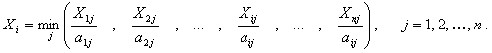
В этом выражении учитываются только затраты промежуточных продуктов, затраты факторов производства опущены. Следовательно, для ответа на поставленный вопрос мы приходим к необходимости отыскания решения X1, X2, … , Xn системы линейных уравнений:
| (9-7) |
Чтобы упростить вид этого выражения, прибегнем к матричному представлению:
X = AX + F, | (9-8) |
где

Полученная формула и есть леонтьевская модель межотраслевого баланса или линейная модель межотраслевого баланса.
Решаем систему уравнений (9-8) относительно X. Получаем:
X-AX=F для любого вектора конечного спроса F. Учитывая, что X=IX, где I – единичная матрица:
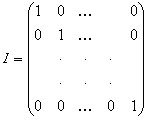
можно записать:
IX-AX=(I-A)X=F
Умножая левую и правую части полученного равенства на матрицу (I-A)-1 (обратную к матрице (I-A)) имеем:
X = (I – A)-1F. | (**) |
Матрица коэффициентов прямых затрат А соответствует таблице коэффициентов аij, и ясно, что далеко не для всякой матрицы А система уравнений (9-8) имеет положительное решение. Легко построить матрицу, для которой будет невозможно подобрать пару положительных векторов X и F, удовлетворяющих (9-8). Например, матрица А с элементами аij>1. В этом случае для любого вектора X>0 выполнено неравенство: AX>X, следовательно, AX+F>0 при F>0 и значит не существует X>0, удовлетворяющего системе уравнений X=AX+F.
Матрица А характеризует экономику производства, и естественно потребовать, чтобы можно было произвести хотя бы один набор конечных продуктов. Для существования решения достаточно, чтобы выполнялось условие Хаукинса-Саймона, т.е. неотрицательная квадратная матрица А являлась продуктивной (productive), т.е. существовал хотя бы один вектор X > 0, такой, что Х > АХ, или в преобразованном виде (I – A)X > 0.
Г.Г.Забудский формулирует теорему, которая оправдывает выделение класса продуктивных матриц.
Теорема: для того, чтобы линейная модель межотраслевого баланса X=AX+F имела решение при любом неотрицательном F необходимо и достаточно, чтобы продуктивной была матрица прямых затрат А. Это решение единственно.
Существует несколько способов проверки продуктивности матрицы А: критерии продуктивности (необходимые и достаточные условия), а также достаточные условия (т.е. если они выполняются, то А – продуктивна, если нет – нельзя делать вывод о непродуктивности матрицы А).
Критерии:
Матрица А продуктивна тогда и только тогда, когда существует матрица (I-А)-1 и она неотрицательна. Неотрицательная матрица А продуктивна тогда и только тогда, когда (I-А) имеет n положительных последовательных главных миноров.
Достаточные условия:
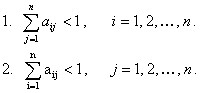
Экономический смысл условия Хаукинса-Саймона заключается в следующем: экономическая система, в которой каждая отрасль функционирует, непосредственно или косвенно потребляя продукцию других отраслей, должна быть способна обеспечивать не только саму себя, но и осуществлять положительные поставки для конечного спроса и при этом любая из ее подсистем должна быть способна осуществлять то же самое. Если хотя бы одна из подсистем не может удовлетворить данное требование, она неизбежно вызовет утечку, которая нарушит способность самоподдержки всей системы – в математической экономике и теории межотраслевых моделей это свойство и называется продуктивностью.
Матрица В=(I-А)-1 называется обратной матрицей Леонтьева или, по аналогии с кейнсианской концепцией мультипликатора, матричным мультипликатором, или мультипликатором Леонтьева. Обратная матрица Леонтьева В есть, собственно, матрица коэффициентов полных затрат. Экономический смысл её элементов bij заключается в следующем: коэффициент bij показывает потребность в валовом выпуске продукции отрасли i для производства единицы конечной продукции отрасли j. Таким образом, bij в сущности есть мультипликатор, показывающий эффект распространения спроса, первоначальным источником которого является конечный спрос на продукцию.
Доказано, что:
I + A + A2 + … + Ak + … = (I – A)-1 | (***) |
Из выражений (**) и (***) получаем:
X = (I – A)-1F = (I + A + A2 + … + Ak + …)F,
причём AF есть результат первичного эффекта распространения, A2F – вторичного и т.д. Из предыдущего соотношения следует, что решение (9-8) можно получить итерационно (по методу Якоби):
X(k+1) = AX(k) + F. | (9-9) |
Подставив в (9-9) в качестве исходного итеративного значения X0 = F, мы рассчитаем эффект мультипликации, порождаемый конечным спросом; задавая другие исходные неотрицательные значения, сможем оценить полученные результаты с экономической точки зрения.