Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, эти данные являются значениями случайной величины.
Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.
При исследовании взаимосвязей между экономическими показателями на основе статистических данных, часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).
Пример функциональной зависимости – выпуск продукции и ее потребление в условиях дефицита.
Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем работы работают лучше молодых, но под влиянием дополнительных факторов – образование, здоровье и т.д. эта зависимость может быть искажена.
Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами называется корреляционным анализом. Основная задача корреляционного анализа – это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) показателями (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов.
Характер связи между показателями определяется по корреляционному полю. Если Y — зависимый признак, а Х — независимый, то отметив каждый случай X(i) с координатами xi и yi получим корреляционное поле.
Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах от минус единицы до плюс единицы. Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае, если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от — 0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полной ее отсутствии.
Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами.
Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна.
Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности, точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию) – линию регрессии.
По числу факторов различают одно-, двух — и многофакторные уравнения регрессии.
По характеру связи однофакторные уравнения регрессии подразделяются на:
а) линейные:
![]()
![]() ,
,
где X – экзогенная (независимая) переменная;
Y – эндогенная (зависимая, результативная) переменная;
a, b – параметры.
б) степенные:
![]()
![]()
в) показательные:
![]()
г) прочие.
Определение параметров линейного однофакторного уравнения регрессии
Пусть у нас имеются данные о доходах (X) и спрос на некоторый товар (Y) за ряд лет (n)
ГОД n | ДОХОД X | СПРОС Y |
1 | x1 | y1 |
2 | x2 | y2 |
3 | x3 | y3 |
… | … | … |
n | xn | yn |
Предположим, что между X и Y существует линейная взаимосвязь, т.е.
![]()
Для того, чтобы найти уравнение регрессии, прежде всего нужно исследовать тесноту связи между случайными величинами X и Y, т.е. корреляционную зависимость.
Пусть:
x![]() , х
, х![]() , . . . ,хn — совокупность значений независимого, факторного признака;
, . . . ,хn — совокупность значений независимого, факторного признака;
y![]() , y
, y![]() . . . ,yn – совокупность соответствующих значений зависимого, результативного признака;
. . . ,yn – совокупность соответствующих значений зависимого, результативного признака;
n – количество наблюдений.
Для нахождения уравнения регрессии вычисляются следующие величины:
Средние значения
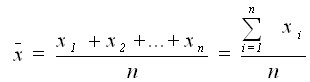 для экзогенной переменной.
для экзогенной переменной.
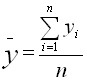 для эндогенной переменной$
для эндогенной переменной$
2. Отклонения от средних величин
![]() ,
, 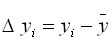 $
$
Величины дисперсии и среднего квадратичного отклонения
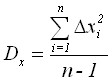 ,
, 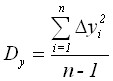 .
.
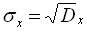
![]()
Величины дисперсии и среднего квадратичного отклонения характеризуют разброс наблюдаемых значений вокруг среднего значения. Чем больше дисперсия, тем больше разброс.
Вычисление корреляционного момента (коэффициента ковариации):
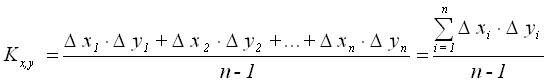
Корреляционный момент отражает характер взаимосвязи между x и y. Если ![]() , то взаимосвязь прямая. Если
, то взаимосвязь прямая. Если ![]() , то взаимосвязь обратная.
, то взаимосвязь обратная.
Коэффициент корреляции вычисляется по формуле:
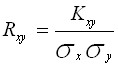 .
.
Доказано, что коэффициент корреляции находится в интервале от минус единицы до плюс единицы (![]() ). Коэффициент корреляции в квадрате (
). Коэффициент корреляции в квадрате (![]() ) называется коэффициентом детерминации.
) называется коэффициентом детерминации.
Если ![]() , то вычисления продолжаются.
, то вычисления продолжаются.
Вычисления параметров регрессионного уравнения.
Коэффициент b находится по формуле:
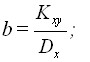
После чего можно легко найти параметр a:
![]()
Коэффициенты a и b находятся методом наименьших квадратов, основная идея которого состоит в том, что за меру суммарной погрешности принимается сумма квадратов разности (остатков) между фактическими значениями результативного признака ![]() и его расчетными значениями
и его расчетными значениями ![]() , полученными при помощи уравнения регрессии
, полученными при помощи уравнения регрессии
![]() .
.
При этом величины остатков находятся по формуле:
![]() , где
, где
![]() фактическое значение y;
фактическое значение y;
![]() расчетное значение y.
расчетное значение y.
Пример. Пусть у нас имеются статистические данные о доходах (X) и спросе (Y). Необходимо найти корреляционную зависимость между ними и определить параметры уравнения регрессии.
ГОД n | ДОХОД X | СПРОС Y |
1 | 10 | 6 |
2 | 12 | 8 |
3 | 14 | 8 |
4 | 16 | 10,3 |
5 | 18 | 10,5 |
6 | 20 | 13 |
Предположим, что между нашими величинами существует линейная зависимость.
Тогда расчеты лучше всего выполнить в Excel, используя статистические функции;
СРЗНАЧ – для вычисления средних значений;
ДИСП – для нахождения дисперсии;
СТАНДОТКЛОН – для определения среднего квадратичного отклонения;
КОРЕЛЛ – для вычисления коэффициента корреляции.
Корреляционный момент можно вычислить, найдя отклонения от средних значений для ряда X и ряда Y , затем при помощи функции СУММПРОИЗВ определить сумму их произведений, которую необходимо разделить на n-1.
Результаты вычислений можно свести в таблицу.
Параметры линейного однофакторного уравнения регрессии
Показатели | X | Y |
Среднее значение | 15 | 9,3 |
Дисперсия | 14 | 6,08 |
Среднее квадр. отклонение | 3,7417 | 2,4658 |
Корреляционный момент | 8,96 | |
Коэффициент корреляции | 0,9712 | |
Параметры | b=0,64 | a = — 0,3 |
В итоге наше уравнение будет иметь вид:
y = — 0.3 + 0.64x
Используя это уравнение, можно найти расчетные значения Y и построить график (рис. 2.1).
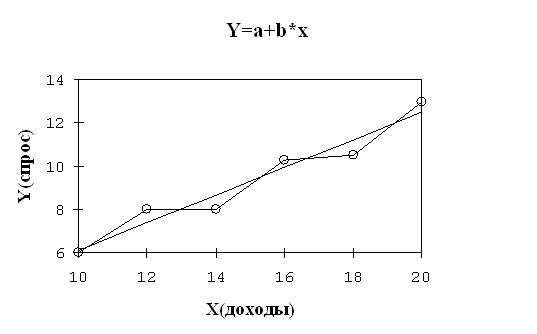
Рис. 2.1. Фактические и расчетные значения ![]()
Ломаная линия на графике отражает фактические значения Y, а прямая линия построена с помощью уравнения регрессии и отражает тенденцию изменения спроса в зависимости от дохода.
Однако встает вопрос, насколько значимы параметры a и b? Какова величина погрешности?
Оценка величины погрешности линейного однофакторного уравнения
Обозначим разность между фактическим значением результативного признака и его расчетным значением как ![]() :
:
![]() , где
, где
![]() фактическое значение y;
фактическое значение y;
![]() расчетное значение y,
расчетное значение y,
![]() – разность между ними.
– разность между ними.
В качестве меры суммарной погрешности выбрана величина:
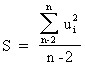 .
.
Для нашего примера S = 0.432.
Поскольку ![]() (среднее значение остатков) равно нулю, то суммарная погрешность равна остаточной дисперсии:
(среднее значение остатков) равно нулю, то суммарная погрешность равна остаточной дисперсии:
Остаточная дисперсия находится по формуле:
![]()
Для нашего примера![]() . Можно показать, что
. Можно показать, что
![]() .
.
Если ![]()
![]() то
то ![]()
![]() то
то ![]()
Таким образом, ![]() .
.
Легко заметить, что если ![]() , то
, то
![]()
Это соотношение показывает, что в экономических приложениях допустимая суммарная погрешность может составить не более 20% от дисперсии результативного признака ![]() .
.
Стандартная ошибка уравнения находится по формуле:
![]() , где
, где
![]() – остаточная дисперсия. В нашем случае
– остаточная дисперсия. В нашем случае ![]() .
.
Относительная погрешность уравнения регрессии вычисляется как:
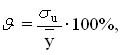
где ![]() стандартная ошибка;
стандартная ошибка;
![]() – среднее значение результативного признака.
– среднее значение результативного признака.
В нашем случае ![]() = 7.07%.
= 7.07%.
Если величина ![]() мала и отсутствует автокорреляция остатков, то прогнозные качества оцененного регрессионного уравнения высоки.
мала и отсутствует автокорреляция остатков, то прогнозные качества оцененного регрессионного уравнения высоки.
Стандартная ошибка коэффициента b вычисляется по формуле:
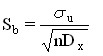
В нашем случае она равна ![]() .
.
Для вычисления стандартной ошибки коэффициента a используется формула:
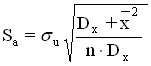
В нашем примере ![]() .
.
Стандартные ошибки коэффициентов используются для оценивания параметров уравнения регрессии.
Коэффициенты считаются значимыми, если
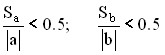
В нашем примере 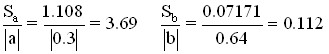
Коэффициент а не значим, т.к. указанное отношение больше 0.5, а относительная погрешность уравнения регрессии слишком высока – 26.7%.
Стандартные ошибки коэффициентов используются также для оценки статистической значимости коэффициентов при помощи t – критерия Стьюдента. Значения t – критерия Стьюдента содержатся в справочниках по математической статистике. В таблице 2.1 приводятся его некоторые значения.
Далее находятся максимальные и минимальные значения параметров (![]() ) по формулам:
) по формулам:
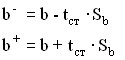
Таблица 2.1
Некоторые значения t – критерия Стьюдента
Степени свободы | Уровень доверия (с) | |
(n-2) | 0,90 | 0,95 |
1 | 6,31 | 12,71 |
2 | 2,92 | 4,30 |
3 | 2,35 | 3,18 |
4 | 2,13 | 2,78 |
5 | 2,02 | 2,57 |
Для нашего примера находим:
![]()
![]()
![]()
![]()
Если интервал (![]() ) достаточно мал и не содержит ноль, то коэффициент b является статистически значимым на с – процентном доверительном уровне.
) достаточно мал и не содержит ноль, то коэффициент b является статистически значимым на с – процентном доверительном уровне.
Аналогично находятся максимальные и минимальные значения параметра а. Для нашего примера:

Коэффициент а не является статистически значимым, т.к. интервал (![]() ) велик и содержит ноль.
) велик и содержит ноль.
Вывод: полученные результаты не являются значимыми и не могут быть использованы для прогнозных расчетов. Ситуацию можно поправить следующими способами:
а) увеличить число n;
б) увеличить количество факторов;
в) изменить форму уравнения.
Проблема автокорреляции остатков. Критерий Дарбина-Уотсона
Часто для нахождения уравнений регрессии используются динамические ряды, т.е. последовательность экономических показателей за ряд лет (кварталов, месяцев), следующих друг за другом.
В этом случае имеется некоторая зависимость последующего значения показателя, от его предыдущего значения, которое называется автокорреляцией. В некоторых случаях зависимость такого рода является весьма сильной и влияет на точность коэффициента регрессии.
Пусть уравнение регрессии построено и имеет вид:
![]()
![]() – погрешность уравнения регрессии в год t.
– погрешность уравнения регрессии в год t.
Явление автокорреляции остатков состоит в том, что в любой год t остаток ![]() не является случайной величиной, а зависит от величины остатка предыдущего года
не является случайной величиной, а зависит от величины остатка предыдущего года ![]() . В результате при использовании уравнения регрессии могут быть большие ошибки.
. В результате при использовании уравнения регрессии могут быть большие ошибки.
Для определения наличия или отсутствия автокорреляции применяется критерий Дарбина-Уотсона:
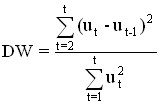 .
.
Возможные значения критерия DW находятся в интервале от 0 до 4. Если автокорреляция остатков отсутствует, то DW≈2.
Построение уравнения степенной регрессии
Уравнение степенной агрессии имеет вид:
![]() , где
, где
a, b – параметры, которые определяются по данным таблицы наблюдений.
Таблица наблюдений составлена и имеет вид:
x | x1 | x2 | … | xn |
y | y1 | y2 | … | yn |
Прологарифмируем исходное уравнение и в результате получим:
![]() ln y = ln a + b⋅ln x .
ln y = ln a + b⋅ln x .
Обозначим ln y через ![]() , ln a как
, ln a как ![]() , а ln x как
, а ln x как ![]() .
.
В результате подстановки получим:
![]()
Данное уравнение есть ничто иное, как уравнение линейной регрессии, параметры которого мы умеем находить.
Для этого прологарифмируем исходные данные:
ln x | ln x1 | ln x2 | … | ln xn |
ln y | ln y1 | ln y2 | … | ln yn |
Далее необходимо выполнить известные нам вычислительные процедуры по нахождению коэффициентов a и b, используя прологарифмированные исходные данные. В результате получим значение коэффициента b и ![]() . Параметр a можно найти по формуле:
. Параметр a можно найти по формуле:
![]() .
.
В этих же целях можно воспользоваться функцией EXP в Excel.
Двухфакторные и многофакторные уравнения регрессии
Линейное двухфакторное уравнение регрессии имеет вид:
![]() ,
,
где ![]() — параметры;
— параметры;
![]() – экзогенные переменные;
– экзогенные переменные;
y – эндогенная переменная.
Идентификацию этого уравнения лучше всего производить с использованием функции Excel ЛИНЕЙН.
Степенное двухфакторное уравнение регрессии имеет вид:
![]()
где ![]() — параметры;
— параметры;
![]() – экзогенные переменные;
– экзогенные переменные;
Y – эндогенная переменная.
Для нахождения параметров этого уравнения его необходимо прологарифмировать. В результате получим:
![]()
![]() .
.
Идентификацию этого уравнения также лучше всего производить с использованием функции Excel ЛИНЕЙН. Следует помнить, что мы получим не параметр a, а его логарифм, которое следует преобразовать в натуральное число.
Линейное многофакторное уравнения регрессии имеет вид:
![]()
где ![]() n — параметры;
n — параметры;
![]() n – экзогенные переменные;
n – экзогенные переменные;
y – эндогенная переменная.
Идентификацию этого уравнения также лучше всего производить с использованием функции Excel ЛИНЕЙН.