The method of determining the seasonal component (in relation to the multiplicative model, it is often called the seasonality index) is in many respects similar to the additive model. As in the previous case, centered moving averages are determined and seasonal deviations are found with their help. But unlike the additive model, seasonal deviations are defined as the quotient of dividing the actual values of the series 
by the corresponding moving averages. The second difference is the finding of seasonal components by the obtained average seasonal deviations 
. To prevent distortions of 
the trend when isolating seasonal fluctuations from the initial series, it is necessary that the sum of the seasonal components be equal to the period of seasonal fluctuations, i.e. the condition is met: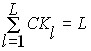 
.
In case of its non-fulfillment, a correction factor k determined by the formula:
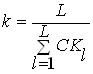
Seasonal components are defined as the products of the corresponding average seasonal deviations by the correction factor: 
.
An example of calculating seasonal components for a multiplicative model is given in Tables 4 – 5.
Table 4. Calculation of seasonal deviations 
.
N | Y(t) | Moving average, L=4 | Centered moving average | Seasonal variations | L |
1 | 72 | 1 | |||
2 | 100 | 2 | |||
3 | 90 | 81.5 | 81.25 | 1.108 | 3 |
4 | 64 | 81.0 | 80.00 | 0.800 | 4 |
5 | 70 | 79.0 | 77.75 | 0.900 | 1 |
6 | 98 | 76.5 | 75.75 | 1.215 | 2 |
7 | 80 | 75.0 | 74.00 | 1.081 | 3 |
8 | 58 | 73.0 | 71.50 | 0.811 | 4 |
9 | 62 | 70.0 | 68.50 | 0.905 | 1 |
10 | 80 | 67.0 | 65.75 | 1.217 | 2 |
11 | 68 | 64.5 | 63.25 | 1.075 | 3 |
12 | 48 | 62.0 | 59.5 | 0.807 | 4 |
13 | 52 | 57.0 | 54.75 | 0.950 | 1 |
14 | 60 | 52.5 | 50.25 | 1.194 | 2 |
15 | 50 | 48.0 | 3 | ||
16 | 30 | 4 |
Table 5. Calculation of the seasonal component 
.
Index | Year | Block number l | ||
1 | 2 | 3 | 4 | |
1 | – | – | 1.108 | 0.800 |
2 | 0.900 | 1.215 | 1.081 | 0.817 |
3 | 0.905 | 1.217 | 1.075 | 0.807 |
4 | 0.950 | 1.194 | – | – |
Seasonal average deviation | 0.918 | 1.209 | 1.088 | 0.808 |
Sum of seasonal average deviations | 4.023 | |||
Correction coefficient k | 4 / 4.023= 0.9943 | |||
Seasonal component | 0.913 | 1.202 | 1.082 | 0.803 |
To isolate the seasonal component from the original series 
, it is necessary to divide each of its points into the corresponding seasonal component, i.e. to find the quotient 
, which will be the product of the trend and the free term 
.