First, seasonal deviations from the intended trend are found for each point of the time series, for this:
– there are moving averages with an averaging period equal to L;
– if the period of seasonal fluctuations is an even number, then the resulting moving averages are interinterfall and in order to obtain centered moving averages, the resulting averages are averaged again, but this time with an averaging period of two;
– for each time interval, the seasonal deviation of the SKt is found as the difference between the actual values and the corresponding averages, i.e.:
![]() .
.
The obtained seasonal deviations are the basis for calculating the normalized seasonal components of Sl for each interval from the period of seasonal variation L. To do this, the obtained deviations ![]() are grouped by the same numbers of points in the period of seasonal fluctuations and in each of the received L groups there are average values of seasonal deviations
are grouped by the same numbers of points in the period of seasonal fluctuations and in each of the received L groups there are average values of seasonal deviations ![]() . so that the condition is met:
. so that the condition is met:
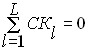 .
.
As a rule, this condition is never met, so a correction factor k is introduced equal to:
 ;
;
The seasonal component for each point of the seasonal period, taking into account the correction coefficient, will be equal to:
![]()
Tables 2 to 3 provide an example illustrating the definition of the seasonal component from the additive model.
Table 2. Calculation of seasonal deviations from the trend.
N | Y(t) | Moving average, L=4 | Centered moving average | Seasonal variations | L |
1 | 6.0 | 1 | |||
2 | 4.4 | 2 | |||
3 | 5.0 | 6.10 | 6.250 | -1.250 | 3 |
4 | 9.0 | 6.40 | 6.450 | 2.550 | 4 |
5 | 7.2 | 6.50 | 6.625 | 0.575 | 1 |
6 | 4.8 | 6.75 | 6.875 | -2.075 | 2 |
7 | 6.0 | 7.00 | 7.100 | -1.100 | 3 |
8 | 10.0 | 7.20 | 7.300 | 2.700 | 4 |
9 | 8.0 | 7.40 | 7.450 | 0.550 | 1 |
10 | 5.6 | 7.50 | 7.625 | -2.025 | 2 |
11 | 6.4 | 7.75 | 7.875 | -1.475 | 3 |
12 | 11.0 | 8.00 | 8.125 | 2.875 | 4 |
13 | 9.0 | 8.25 | 8.325 | 0.675 | 1 |
14 | 6.6 | 8.40 | 8.375 | -1.775 | 2 |
15 | 7.0 | 8.35 | 3 | ||
16 | 10.8 | 4 |
Table 3. Calculation of the seasonal component.
Index | Block number l | |||
1 | 2 | 3 | 4 | |
1 year | – | – | -1.250 | 2.550 |
2 year | 0.575 | -2.075 | -1.100 | 2.700 |
3 year | 0.550 | -2.025 | -1.475 | 2.875 |
4 year | 0.675 | -1.775 | – | – |
Seasonal average deviation | 0.600 | -1.958 | -1.275 | 2.708 |
Sum of seasonal average deviations | 0.075 | |||
Correction coefficient k | 0.075 / 4 = 0.01875 | |||
Seasonal component | 0.581 | -1.977 | -1.275 | 2.708 |
To isolate the seasonal component from the original series yt, it is necessary to subtract from each point of this series the corresponding seasonal component, i.e. to find the difference ![]() that will represent the sum of the trend and the free term
that will represent the sum of the trend and the free term ![]() . The resulting time series without seasonal fluctuations is used to find the equation describing the trend.
. The resulting time series without seasonal fluctuations is used to find the equation describing the trend.