After seasonal variations have been excluded from the original time series, the trend of the time series is determined in the traditional way. The type of dependence for the trend (linear or nonlinear) is selected and then the coefficients of the regression equation are determined by the method of least squares.
However, due to the fact that the time series is a sequence of values ordered by an independent variable with a constant step of change, there are additional opportunities to solve the problem of selecting the most suitable type of trend. For this purpose, smoothing of the studied series without seasonal fluctuations with moving averages with different smoothing intervals can be used. The larger the smoothing interval, the smoother the curve becomes and the more obvious is the most appropriate law for the trend. But at the same time, the smoothed series becomes shorter (the number of points equal to the anti-aliasing period disappears) and the more the smoothed curve breaks away from the original series.
In addition to visual selection, various analytical methods can also be used.
The predictive values of the 
variable are determined by:
for the additive model 
;
for the multiplicative model 
.
Predicting the random component
After you have built a predictive model that includes the trend and seasonal variations, it is necessary to find and analyze the residues 
for the additive model and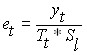 
for the multiplicative model. If the construction of the forecast model is carried out without errors and the initial data are not characterized by the influence of previous values on subsequent ones (the phenomenon of autoregression), then the residues should be a stationary time series. Stationary time series is a series of values, of which are a random variable, i.e. the average and variance of such a series remain unchanged for a long period of time. With regard to residues, this means that their time graph is a cloud of points located symmetrically relative to the abscissa axis, the boundaries of this cloud are parallel to the axis and no patterns in their appearance are observed between the points.
The proximity of the residues to the stationary time series indicates that a radical improvement in the forecast model is no longer possible, but, nevertheless, it is possible to slightly increase the accuracy of forecasting by predicting the balances themselves. The easiest way to predict the residues is in two ways – with the help of a moving average and with the help of an exponentially weighted average.
When forecasting using a moving average, the forecast value of the balance (deviations of the forecast value 
from its future actual value 
) is carried out according to the formula:
where: 
residues in the 
previous steps from t-n+1 to t.
Thus, in this case, not the central moving averages are used, but the end moving averages, i.e. the averages calculated at the current point and n previous points. The fewer points used to calculate the moving average, the stronger the forecast responds to the latest values (recent errors).
When forecasting with an exponentially weighted average, the forecast value of the residue is determined not on the basis of n last points, but on all previous points, but in this case the weight of these points decreases by exponential dependence. One of the formulas for calculating the exponentially weighted average is:
where: 
is an anti-aliasing parameter that determines the rate at which the weight of residues for previous points decreases as they are removed to the beginning of the series.
Typically, the anti-aliasing 
option is selected between 0.05 ÷ 0.3. The higher the anti-aliasing parameter value, the stronger the forecast responds to recent changes. Most often, it is chosen as 0.2, which is approximately equivalent to a 9-point moving average.
Forecasting with a moving average and an exponentially weighted average give approximately the same results, but forecasting with an exponentially weighted average works better in situations where the series is not completely stationary, i.e. we were not able to take into account all the trends in the forecast model. As a rule, forecasting using not only the trend and the seasonal component, but also the forecast of the balance allows you to somewhat reduce the variance of forecasting errors. The predictive equations will be of the form:
– for the additive model and
– for the multiplicative model.
Security questions
What is a time series? How is a time series different from a cross-data sample? What components are commonly observed in time series? What is the seasonal component of the time series? When modeling a time series, why is it necessary to first allocate a seasonal component? What are non-periodic fluctuations and how are they handled when they cannot be isolated? What is the difference between additive and multiplicative models and how to determine in practice which of the models is more suitable for the predicted time series How to determine the length of the period of seasonal fluctuations? What is the interintervaline moving average and when does it occur? What condition should seasonal deviations in the additive model correspond to and how should they be met? What condition should seasonal deviations in the multiplicative model meet and how should they be met? What data is used to determine the trend of the time series? How to exclude seasonal fluctuations from the time series? What is the Seasonality Index? What is a stationary time series and how to determine how close the remains are to it? What is the end moving average and what is it used for? What is an exponentially weighted moving average and what is it used for? What is the anti-aliasing parameter and how does it affect the accuracy of forecasting? What does residue forecasting do? Which of the methods of forecasting residues is more preferable and under what conditions?