После того как из исходного временного ряда исключены сезонные колебания, определение тенденции временного ряда осуществляется традиционным способом. Выбирается вид зависимости для тенденции (линейная или нелинейная) и далее методом наименьших квадратов определяются коэффициенты регрессионного уравнения.
При этом благодаря тому, что временной ряд представляет собой упорядоченную по независимой переменной последовательность значений с постоянным шагом изменения, появляются дополнительные возможности по решению задачи выбора наиболее подходящего вида тенденции. Для этих целей может быть использовано сглаживание исследуемого ряда без сезонных колебаний скользящими средними с различными интервалами сглаживания. Чем больше интервал сглаживания, тем более гладкой становится сглаженная кривая и тем более очевидным становится наиболее подходящий закон для тенденции. Но при этом сглаженный ряд становится все более коротким (число точек, равное периоду сглаживания пропадает) и тем больше сглаженная кривая отрывается от исходного ряда.
Помимо визуального подбора могут применяться и различные аналитические методы.
Прогнозные значения переменной ![]() определяются:
определяются:
для аддитивной модели ![]() ;
;
для мультипликативной модели ![]() .
.
Прогнозирование случайной составляющей
После того как построена прогнозная модель, включающая тенденцию и сезонные колебания необходимо найти и проанализировать остатки ![]() для аддитивной модели и
для аддитивной модели и 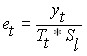 для мультипликативной модели. Если построение прогнозной модели выполнено без ошибок и для исходных данных не характерно влияние предшествующих значений на последующие (явление авторегресии), то остатки должны представлять собой стационарный временной ряд. Стационарный временной ряд – это ряд значения, которого являются случайной величиной, т.е. средняя и дисперсия такого ряда на длительном промежутке времени остаются неизменными. Применительно к остаткам это означает, что их график во времени представляет собой облако точек, расположенных симметрично относительно оси абсцисс, границы этого облака параллельны оси и между точками не наблюдаются какие либо закономерности в их появлении.
для мультипликативной модели. Если построение прогнозной модели выполнено без ошибок и для исходных данных не характерно влияние предшествующих значений на последующие (явление авторегресии), то остатки должны представлять собой стационарный временной ряд. Стационарный временной ряд – это ряд значения, которого являются случайной величиной, т.е. средняя и дисперсия такого ряда на длительном промежутке времени остаются неизменными. Применительно к остаткам это означает, что их график во времени представляет собой облако точек, расположенных симметрично относительно оси абсцисс, границы этого облака параллельны оси и между точками не наблюдаются какие либо закономерности в их появлении.
Близость остатков к стационарному временному ряду свидетельствует о том, что кардинальное улучшение прогнозной модели уже не возможно, но, тем не менее, несколько повысить точность прогнозирования возможно за счет прогнозирования самих остатков. Наиболее просто прогнозировать остатки можно двумя способами – с помощью скользящей средней и с помощью экспоненциально взвешенной средней.
При прогнозировании с помощью скользящей средней прогнозное значение остатка (отклонения прогнозного значения ![]() от его будущего фактического значения
от его будущего фактического значения ![]() ) осуществляется по формуле:
) осуществляется по формуле:
![]()
где: ![]() остатки на
остатки на ![]() предыдущих шагах от t-n+1 до t.
предыдущих шагах от t-n+1 до t.
Таким образом, в этом случае используются не центральные скользящие средние, а концевые скользящие средние, т.е. средние, рассчитываемые по текущей точке и n предыдущих точек. Чем меньшее число точек использовано для расчета скользящей средней, тем сильнее прогноз реагирует на последние значения (на последние ошибки).
При прогнозировании с помощью экспоненциально взвешенной средней прогнозное значение остатка определяется не на основании n последних точек, а по всем предшествующим точкам, но в этом случае вес этих точек убывает по экспоненциальной зависимости. Одна из формул для подсчета экспоненциально взвешенной средней имеет вид:
![]()
![]()
где: ![]() — параметр сглаживания, определяющий скорость с которой уменьшается вес остатков для предыдущих точек по мере их удаления к началу ряда.
— параметр сглаживания, определяющий скорость с которой уменьшается вес остатков для предыдущих точек по мере их удаления к началу ряда.
Обычно параметр сглаживания ![]() выбирается в пределах от 0.05 ÷ 0.3. Чем большее значение параметра сглаживания, тем сильнее прогноз реагирует на последние изменения. Наиболее часто его выбирают равным 0.2, что примерно равноценно скользящей средней по 9 точкам.
выбирается в пределах от 0.05 ÷ 0.3. Чем большее значение параметра сглаживания, тем сильнее прогноз реагирует на последние изменения. Наиболее часто его выбирают равным 0.2, что примерно равноценно скользящей средней по 9 точкам.
Прогнозирование с помощью скользящей средней и экспоненциально взвешенной средней дают примерно одинаковые результаты, но прогнозирование с помощью экспоненциально взвешенной средней лучше работает в ситуациях когда ряд не до конца стационарен, т.е. нам не удалось учесть в прогнозной модели все тенденции. Как правило прогнозирование с использованием не только тенденции и сезонной составляющей, но и на прогноз остатка позволяет несколько уменьшить дисперсию ошибок прогнозирования. Прогнозные уравнения при этом будут иметь вид:
![]() — для аддитивной модели и
— для аддитивной модели и
![]() — для мультипликативной модели.
— для мультипликативной модели.
Контрольные вопросы
Что такое временной ряд? Чем временной ряд отличается от выборки перекрестных данных? Какие компоненты обычно наблюдаются во временных рядах? Что такое сезонная компонента временного ряда? Почему при моделировании временного ряда необходимо вначале выделить сезонную компоненту? Что такое непериодические колебания и как с ними поступают в тех случаях, когда их невозможно выделить? Чем отличаются аддитивная и мультипликативные модели и как на практике определить какая из моделей больше подходит к прогнозируемому временному ряду Как определить длину периода сезонных колебаний? Что такое межинтервальная скользящая средняя и в каких случаях она возникает? Какому условию должны соответствовать сезонные отклонения в аддитивной модели и как их обеспечить? Какому условию должны соответствовать сезонные отклонения в мультипликативной модели и как их обеспечить? Какие данные используются для определения тенденции временного ряда? Как исключить сезонные колебания из временного ряда? Что такое индекс сезонности? Что такое стационарный временной ряд и как определить насколько близки к нему остатки? Что такое концевая скользящая средняя и для чего она применяется? Что такое экспоненциально взвешенная скользящая средняя и для чего она применяется? Что такое параметр сглаживания и как он влияет на точность прогнозирования? Что дает прогнозирование остатков? Какой из методов прогнозирования остатков более предпочтителен и при каких условиях?