На практике чаще всего известны не только значения прогнозируемой величины для объектов аналогичных объекту прогнозирования или сама эта величина в прошлом, но и другие величины, влияющие на прогнозируемую или изменяющиеся совместно с ней. В этом случае говорят о наличии связи между этими величинами и использование знаний об этой связи, позволяет значительно повысить точность по сравнению с прогнозированием по выборке.
Рассмотрим простейший случай парной зависимости, когда есть прогнозируемая величина и лишь одна величина на нее влияющая.
Будем обозначать искомую прогнозируемую величину через У и называть зависимость переменной, а влияющие на нее переменную через Х и называть независимой переменной.
Связь между зависимой и независимой переменными может быть функциональная, в этом случае каждому значению независимой переменной соответствует одно определенное значение зависимой переменной, графически такая связь выражается линией на графике. Второй вид связи – вероятностная (стохастическая) связь, в этом случае одному значению независимой переменной соответствует несколько значений зависимой переменной. Графически вероятностная связь может быть представлена как некое облако точек (рис.12). Причем частота появления различных значений переменной Y при одном и том же значении ![]() подчиняется какому-то закону, т.е. имеет определенный тип распределения, одинаковый во всем диапазоне значений независимой переменной.
подчиняется какому-то закону, т.е. имеет определенный тип распределения, одинаковый во всем диапазоне значений независимой переменной.
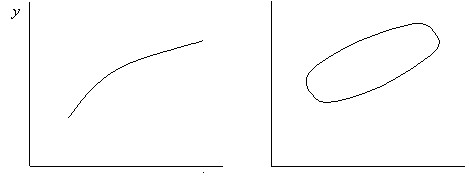
Рис.12. Функциональная (а) вероятностная (б) связь переменных.
Для описания вероятностной связи переменных используются уравнение регрессии. В идеологии регрессионного анализа лежит представление о всех возможных значениях переменных Х и У как о случайных отклонениях от их средних значений ![]() и
и ![]() . Регрессионное уравнение устанавливает связь между отклонениями зависимой и независимой переменных от своих средних значений. Следует особо отметить, что в регрессионном анализе речь идет именно о связи (определенной степени совместности изменения) Y и X, а не зависимости Y от X. Иными словами регрессионный анализ не устанавливает факт влияния X на Y, фактически это может быть и противоположное влияние — Y влияет на X, или обе переменные Y и X зависят от третьей или третьих переменных. Во всех этих случаях будет наблюдаться некоторая согласованность изменения значений X и Y, и эту согласованность можно установить с помощью уравнения регрессии.
. Регрессионное уравнение устанавливает связь между отклонениями зависимой и независимой переменных от своих средних значений. Следует особо отметить, что в регрессионном анализе речь идет именно о связи (определенной степени совместности изменения) Y и X, а не зависимости Y от X. Иными словами регрессионный анализ не устанавливает факт влияния X на Y, фактически это может быть и противоположное влияние — Y влияет на X, или обе переменные Y и X зависят от третьей или третьих переменных. Во всех этих случаях будет наблюдаться некоторая согласованность изменения значений X и Y, и эту согласованность можно установить с помощью уравнения регрессии.
Термин регрессия был введен в позапрошлом веке в результате изучения влияния роста родителей на рост детей. Повсеместно бытует мнение, что у высоких родителей высокие дети. Проверка на большом статистическом материале показала, что в среднем дети высоких родителей имеют рост меньший, чем рост родителей, т.е. рост детей высоких родителей регрессирует, имеет тенденцию возвращаться к среднему росту. А рост детей невысоких родителей прогрессирует – имеет тенденцию приближаться к среднему росту.
Наиболее часто на практике для описания связи между X и Y применяется линейный закон. Соответственно говорят о парной линейной регрессионной зависимости, с ее помощью взаимосвязь между зависимой и независимой переменными описывается следующим образом:
![]()
где:![]() ,
, ![]() — коэффициенты регрессионного уравнения;
— коэффициенты регрессионного уравнения;
![]() — остаточный член.
— остаточный член.
Таким образом, случайная величина Y представляется состоящей из двух частей:
теоретического значения, которое можно рассчитать по известному значению X с использованием формулы ![]() ;
;
и остаточного члена ![]() который представляет собой случайную составляющую которую предсказать невозможно и благодаря которой связь между зависимой и независимой переменными носит вероятностный характер.
который представляет собой случайную составляющую которую предсказать невозможно и благодаря которой связь между зависимой и независимой переменными носит вероятностный характер.
Среди причин появления случайной составляющей ![]() могут быть следующие:
могут быть следующие:
— отсутствие в уравнении регрессии других независимых переменных влияющих на зависимую переменную и не включенных в уравнение вследствие их незнания или отсутствия возможности надежного измерения;
— агрегирование зависимой переменной из нескольких однородных, но все-таки отличающихся друг от друга переменных (прибыль по предприятию представляет собой сумму прибыли по отдельным продуктам производимым этим предприятием, а это схожие, но все-таки разные экономические категории);
— несоответствие избранной теоретической зависимости между зависимой и независимой переменной фактической зависимости;
— ошибки измерения как зависимой, так и независимой переменных.
Во всех этих случаях возникают ошибки, которые приводят к возникновению случайной составляющей.
Общая схема прогнозирования с использованием регрессионной зависимости выглядит следующим образом. По имеющемуся набору ![]() пар значений
пар значений ![]() и
и ![]() необходимо найти параметры уравнения регрессии, а затем с помощью полученного уравнения и нового значения независимой переменной
необходимо найти параметры уравнения регрессии, а затем с помощью полученного уравнения и нового значения независимой переменной ![]() , рассчитать прогнозное значение зависимой переменной
, рассчитать прогнозное значение зависимой переменной ![]() . Поскольку при этом случайную составляющую предсказать не удается, то дополнительно необходимо оценить точность полученного прогноза.
. Поскольку при этом случайную составляющую предсказать не удается, то дополнительно необходимо оценить точность полученного прогноза.