Production is understood as any activity for the use of natural, material, technical and intellectual resources to obtain both material and intangible benefits.
With the development of human society, the nature of production changes. In the early stages of human development, natural, natural, “naturally arising” elements of the productive forces dominated. And man himself at this time was more a product of nature. Production during this period was called natural.
With the development of the means of production and of man himself, the “historically created” material and technical elements of the productive forces begin to prevail. This is the era of capital.
At present, knowledge, technology, intellectual resources of the person himself are of decisive importance. Our epoch is the epoch of informatization, the epoch of the domination of the scientific and technical elements of the productive forces. Possession of knowledge, new technologies is crucial for production. In many developed countries, the task of universal informatization of society is set. The worldwide computer network Internet is developing at an amazing pace.
Traditionally, the role of the general theory of production is performed by the theory of material production, understood as the process of turning production resources into a product. The main productive resources are labor (L) and capital (K). Modes of production or existing production technologies determine how much output is produced at given quantities of labor and capital. Mathematically existing technologies are expressed through a production function. If you denote the volume of output in Y, then the production function can be written:
Y = f(K,L) .
This expression means that the volume of output is a function of the quantity of capital and the quantity of labor. The production function describes many of the currently existing technologies. If the best technology is invented, then at the same cost of labor and capital, the volume of output increases. Consequently, changes in technology change the production function as well.
Methodologically, the theory of production is largely symmetrical to the theory of consumption. However, if in the theory of consumption the main categories are measured only subjectively or are not yet subject to measurement at all, then the main categories of the theory of production have an objective basis and can be measured in certain natural or value units.
Despite the fact that the concept of “production” may seem very broad, vaguely expressed and even vague, since in real life “production” means an enterprise, a construction site, an agricultural farm, a transport enterprise, and a very large organization such as a branch of the national economy, nevertheless, economic and mathematical modeling highlights something common to all these objects. This common is the process of converting primary resources (production factors) into the final results of the process. In connection with the basic and initial concept in the description of an economic object, a “technological method” becomes, which is usually represented as a vector v of input-output, which includes a list of the amounts of resources spent (vector x) and information about the results of their transformation into final products or other characteristics (profit, profitability, etc.). (vector y):
v = (x; y).
The dimension of the vectors x and y, as well as the methods of their measurement (in physical or value units) depend significantly on the problem under study, on the levels at which certain tasks of economic planning and management are set. The set of vectors – technological methods that can serve as a description (from the acceptable point of view of the researcher accuracy) of the production process that is really feasible on some object, is called the technological set V of this object. For certainty, we will assume that the dimension of the cost vector x is N, and the output vector y, respectively, M. Thus, the technological method v is a vector of dimension (M + N), and the technological set 
. Among all the technological methods feasible on the object, a special place is occupied by methods that differ favorably from all others in that they require either less cost with the same output, or correspond to a larger output at the same cost. Those that occupy, in a sense, a marginal position in set V are of particular interest because they are a description of an acceptable and extremely profitable real production process.
Let’s say that a vector 
is preferable to a vector 
with a designation:
,
if the following conditions are true:
1) 
;
2) 
and there is at least one of two things:
(a) There is such a number i0 that 
;
b) there is such a number j0 that 
.
A technological method 
is called efficient if it belongs to the technological set V and there is no other vector 
that would be preferable 
. The above definition means that those methods that cannot be improved on any cost component, on any item of output, without ceasing to be acceptable, are considered effective. The set of all technologically efficient methods are denoted by V*. It is a subset of the technological set V or coincides with it. In essence, the task of planning the economic activity of a production facility can be interpreted as the task of choosing an effective technological method that best suits some external conditions. When solving such a selection problem, the idea of the very nature of the technological set V, as well as its effective subset V *, is quite significant.
In some cases, it is possible to allow within the framework of fixed production the possibility of interchangeability of certain resources (various types of fuel, machines and workers, etc.). At the same time, the mathematical analysis of such productions is based on the premise of the continuum nature of the set V, and consequently on the fundamental possibility of representing the options for mutual substitution with the help of continuous and even differentiated functions defined on V. This approach received its greatest development in the theory of production functions.
Using the concept of an effective technological set, a production function (PF) can be defined as a mapping:
y = f(x) , where 
.
The specified mapping is, generally speaking, multivalued, i.e. the set f(x) contains more than one point. However, for many realistic situations, production functions are unambiguous and even, as mentioned above, differentiated. In the simplest case, the production function is the scalar function of the N arguments:
.
Here, the value of y has, as a rule, a value character, expressing the volume of output produced in monetary terms. The arguments are the amount of resources spent in the implementation of the appropriate effective technological method. Thus, the given ratio describes the boundary of the technological set V, since with a given cost vector (x1,…,xN) it is impossible to produce products in an amount greater than y, and the production of products in an amount smaller than indicated corresponds to an inefficient technological method. The expression for the production function is possible to use to assess the effectiveness of the method of management adopted at this enterprise. In fact, for a given set of resources, it is possible to determine the actual output and compare it with the calculated production function. The resulting difference provides useful material for evaluating efficiency in absolute and relative terms.
The production function is a very useful apparatus of planned calculations and therefore a statistical approach to the construction of production functions for specific economic units is currently developed. In this case, some standard set of algebraic expressions is usually used, the parameters of which are found using the methods of mathematical statistics. Such an approach means, in essence, the evaluation of the production function on the basis of the implicit assumption that the observed production processes are efficient. Among the various types of production functions, linear functions of the form are most often used:
,
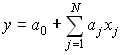since for them it is easy to solve the problem of estimating coefficients according to statistical data, as well as power functions:
,
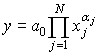for which the problem of finding parameters is reduced to estimating a linear form by switching to logarithms.
In the assumption of the differentiability of the production function at each point of the set X of possible combinations of expendable resources, it is useful to consider some PF-related quantities.
In particular, the differential:
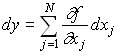
is the change in the cost of output in the transition from the cost of a set of resources x = (x1,…,xN) to a set of x + dx = (x1 + dx1,…,xN + dxN) provided that the efficiency properties of the corresponding technological methods are preserved. Then the value of the partial derivative:
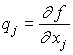
can be interpreted as the marginal (differential) resource efficiency or in other words, the coefficient of marginal productivity, which shows how much output will increase due to an increase in the cost of a resource with the number j by a “small” unit. The value of the marginal productivity of the resource can be interpreted as the upper limit of the price pj, which the production facility can pay for an additional unit of the resource j-th in order not to be at a loss after its acquisition and use. In fact, the expected increase in production in this case will be:
and therefore the ratio
will allow you to get additional profit.
In a short period, when one resource is treated as a constant and the other as a variable, most production functions have the property of a decreasing marginal product. The marginal product of a variable resource is the increase in the total product due to the increase in the use of this variable resource by one.
The marginal product of labor can be written as the difference:
MPL = F(K,L+1) – F(K,L), where
MPL is the ultimate product of labor.
The marginal product of capital can also be written as the difference:
MPK = F(K+1,L) – F(K,L),
Where MPK is the ultimate product of capital.
The characteristic of the production facility is also the value of the average resource efficiency (productivity of the production factor):
,
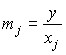having a clear economic meaning of the amount of output per unit of resource used (production factor). Inverse of resource output
,
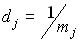commonly referred to as resource intensity because it expresses the amount of resource j required to produce one unit of output in value terms. Such terms as capital intensity, material intensity, energy intensity, labor intensity are very common and understandable, the growth of which is usually associated with the deterioration of the economy, and their decline is considered as a favorable result.
Separate from dividing differential productivity by average:
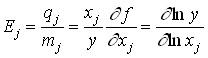
is called the coefficient of elasticity of products according to the production factor j and gives an expression of the relative increase in production (in percentage) with a relative increase in the costs of the factor by 1%. If Ej ≤ 0, then there is an absolute decrease in output with an increase in the consumption of factor j; such a situation may occur when technologically inappropriate products or regimes are used. For example, excessive fuel consumption will lead to an excessive increase in temperature and the chemical reaction necessary for the production of the product will not go. If 0 < Ej ≤ 1, then each subsequent additional unit of the spent resource causes a smaller additional increase in production than the previous one.
If Ej > 1, then the value of incremental (differential) productivity exceeds the average productivity. Thus, an additional unit of resource increases not only the volume of output, but also the average resource efficiency characteristic. So the process of increasing the return on capital occurs when very progressive, efficient machines and devices are put into operation. For a linear production function, the coefficient aj is numerically equal to the value of the differential productivity of the j factor, and for the power function, the exponent of αj makes sense of the coefficient of elasticity over the j-th resource.