Selective observation refers to non-continuous observation. At the heart of this observation is the idea that a randomly selected part of the units can represent the entire population of the phenomenon under study according to the characteristics of interest. The purpose of sampling observation is to obtain information for determining the summary generalizing characteristics of the entire population under study.
Selective observation has a number of advantages over continuous observation:
1. Since part of the units of the population is examined, there will be fewer registration errors, therefore, the information will be more reliable;
2. Selective observation allows you to collect more complete information in a shorter time with less labor and money;
3. When studying some phenomena, it is impossible to conduct a complete observation.
Principles of sampling method theory:
(1) Ensuring randomness consists in the fact that when selecting each of the units of the studied population, an equal opportunity to get into the sample is ensured;
(2) Ensuring a sufficient number of selected units.
The concept of representativeness of the selected population does not mean its full representation on all signs of the population, since this is practically impossible to ensure. The part selected from the entire study population should be representative of those features that are studied or have a significant impact on the formation of composite indicators.
The general population is the entire studied set of units according to the characteristics of interest.
A sample population is a randomly selected part of a general population.
The characteristics of the general and sample populations can serve as the average values of the features, their variance, standard deviation, mode, median, characteristics of an alternative feature.
According to the method of organization, the following types of selective observation (sampling) are distinguished:
1) typical (stratified). Before selection, the units of the general population are preliminarily divided into separate typical groups on a basis essential to the phenomena to be studied. In this case, from each group, a selection is made in proportion to the volume of this group;
2) random. The essence of the random selection of units of the aggregate is that each unit of observation falls into the sample completely by chance – by lot.
Depending on the method of selection of units, the following are distinguished:
selection according to the scheme of the returned ball, which is called re-sampling. In repeated selection, the probability of each individual unit entering the sample remains constant, since after a unit has been selected, it is returned to the population, and it can again be selected; selection according to the scheme of a non-returnable ball, which is called a non-recurring sample. In this case, each selected unit is not returned back to the aggregate.
3) mechanical. The essence of mechanical sampling is that all units of the general population are arranged in some order (ascending or decreasing, geographical location), and then purely mechanically, at a certain interval, units are selected into the sample population;
4) serial. The essence of serial selection is that it is not individual units of the general population that are selected, but whole series of such units; in the selected series, a complete description of all the units included in them is made.
In comparison with the general population, the characteristics of the sample population may have some inaccuracies, discrepancies. Such discrepancies are called statistical observation errors.
Errors of representativeness are the discrepancies between the average values or shares of the feature of the sample and the general population. Errors of representativeness can be systematic and random.
Systematic errors are representativeness errors that arise due to a violation of the scientific principle of selecting units into a sample population. They arise in cases where, as a result of improper organization of selection, the sample population is predominantly the best or worst in relation to a particular feature of the unit.
Random errors of representativeness are inaccuracies that arise from the fact that the sample population does not quite correctly reproduce the structure of the general population.
Errors of representativeness are peculiar only to selective observation. They cannot be completely eliminated, but they can be reduced to negligible sizes. Since a random sampling error results from random differences between the units of the sample and the general population, with a sufficiently large sample size, it will be arbitrarily small.
The ultimate theorems of probability theory allow us to determine the size of random sampling errors. A distinction is made between the average (standard) and marginal sampling errors.
The average sampling error is understood as such a discrepancy between the average sample (
) and the average general population 
that does not exceed 
.
Average sampling error in case of random re-sampling (P.L. Chebyshev’s formula) (μ):
.
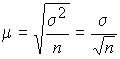decreases with a decrease in the oscillation of the trait, as well as with an increase in the volume of the sample population. Therefore, with a decrease in the oscillation of the trait, it is possible to reduce the volume of the sample population.
Average sampling error in determining the proportion of a feature:
,
where 
is the share of the feature in the general population;
– the number of units in the sample population;
is the variance of the share of the trait.
For non-recurring selection:
to determine the error of the sample average
,
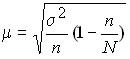where 
is the number of units in the population.
to determine the sampling error
.
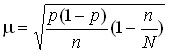The marginal sampling error is called the maximum possible divergence 
, i.e. the maximum error with a given probability of its occurrence.
Marginal error in re-selection:
for medium:
,
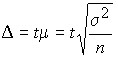where t is the given confidence factor (the multiplicity criterion of the sampling error).
t = 1 P = 0.683
t = 2 P = 0.954
t = 3 P = 0.997
for the share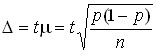 
.
In the case of continuous selection, the marginal sampling errors should be determined by:
for the middle ; for the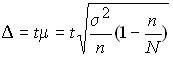 
share .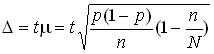 
The marginal sampling error makes it possible to determine the limit values of the characteristics of the general population at a given probability and their confidence intervals:
.
This means that with a given probability, it can be argued that the value of the general average can be expected to 
be within 
.
The relative sampling error is also calculated:
.
One of the important tasks in conducting sample observation is to establish the necessary number of the sample population, i.e. such a number that would provide data sufficiently reflecting the studied properties of the general population.
The required sample 
size is determined depending on the size of the marginal error (
), on the value of the confidence coefficient (t) and on the size of the variance (
).
When re-selecting:
for medium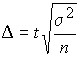 
both sides are squared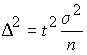 
, therefore 
;
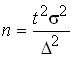for share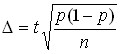 
both sides are 
squared , then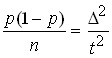 
, therefore .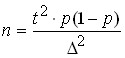 
In case of non-recurring selection:
for the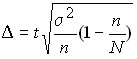 
mean , therefore 
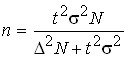; for the fraction 
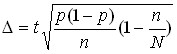, therefore .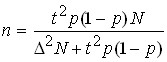
The ultimate goal of sampling is to characterize the general population on the basis of sampling. At the same time, the general population is subject not only to average and relative values, but also to calculate volume indicators for the entire general population on the basis of data obtained as a result of sample observation. The following methods of disseminating sample data to the entire population are used:
1. The method of direct recalculation is based on the fact that the average values or ratios of individual parts obtained as a result of selective observation are multiplied by the number of units of the general population.
2. The method of coefficients is based on the fact that when comparing the data of a complete observation with the data of a sample survey, a coefficient is established that serves to make corrections to the data of a complete observation.