The dual linear programming problem can be formulated as follows:
Find variables yi (i=1,2,… (m) at which the objective function would be minimal
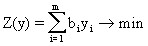 ,
,
without violating the restrictions
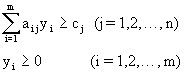
This problem is called dual (symmetric) in relation to the direct problem formulated in the second paragraph of this chapter. However, the converse is also correct, because both tasks are equal. Variables of a dual problem are called objectively conditioned estimates.
The direct and inverse problems of linear programming are interconnected by duality theorems.
The first duality theorem. If both problems have valid solutions, then they have an optimal solution, and the value of the objective functions will be the same:
F(x)=Z(y) or 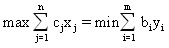 .
.
If at least one of the problems does not have an acceptable solution, then none of them has an optimal solution.
The second duality theorem (complementary non-rigidity theorem). In order for vectors ![]() to be optimal solutions to the direct and dual problem, respectively, it is necessary and sufficient that the following conditions are met:
to be optimal solutions to the direct and dual problem, respectively, it is necessary and sufficient that the following conditions are met:
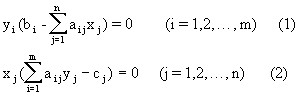
Consequence1. Let the optimal value of some variable of the dual problem be strictly positive
![]() .
.
Then from condition (1) we get:
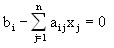 or
or

The economic meaning of these expressions can be interpreted in the following wording. If the objectively conditioned estimate of some resource is greater than zero (strictly positive), then this resource is completely (without residue) consumed in the process of implementing the optimal plan.
Consequence2. Let the condition of strict inequality be fulfilled for the optimal value of some variable xi of the direct problem
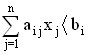 .
.
Then, based on the same first condition (1), we can conclude that yi=0.
Economically, this means that if in the optimal plan some resource is not fully used, then its objectively conditioned assessment is necessarily zero.