Calculation of total labor costs.
However, it would be wrong to limit ourselves to taking into account the costs of an intermediate product (services) for our purposes.
There are still many factors that should be taken into account when assessing internal costs in full. Among them: the costs of labor and capital on production, as well as the cost of resources to overcome the harmful effects of the expansion of production on the environment.
Since regular information that allows the introduction of environmental aspects into the model is not being developed, we will confine ourselves to taking into account the total costs of labor and capital.
The calculation of total labor costs can be carried out through the full salary intensity with the subsequent calculation of the number of employees. For this purpose, let’s return to table. 6.7, which contains the coefficients of direct wage intensity by industry:
![]() and .
and . ![]()
To find the full cost of labor, we will use the ratio:
 (6.5)
(6.5)
Suppose that k=1, j=1,2 (i.e. consider the need for full pay for industry). Then:
L1 = l1⋅b11⋅U1 + l2 ⋅b21 ⋅U1 (6.6)
For agriculture, by analogy, we get:
L2 = l1⋅b12⋅U2 + l2 ⋅b22 ⋅U2 (6.7)
Further, for the economy as a whole, we have:
L = L1 + L2 = l1⋅b11⋅U1 + l2 ⋅b21 ⋅U1 + l1⋅b12⋅U2 + l2 ⋅b22 ⋅U2 =
= l1 (b11⋅У1 + b12 ⋅У1) + l2 (b21⋅У2 + b22 ⋅У2)
In matrix form, this ratio will be recorded as
L = (lj)1⋅V⋅Y or
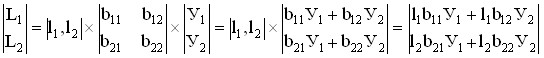
For our case we have (У1=110; У2=-40):
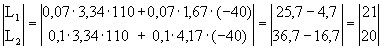
The result, as you can see, coincides with the data of the table. 6.7. accurate to rounding.
The matrix of coefficients of total marginal labour costs thus consists of the following elements:
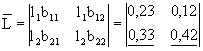
0,56 0,54
Thus, the final product of industry is more wage-intensive than the final product of agricultural production (0.56>0.54). Therefore, from the point of view of labor costs alone, the import of agricultural products is impractical.
Let’s analyze the distribution of total labor costs (by final product):
L(U1) L(U2)
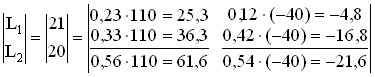
It turns out that the amount of wages required in the national economy for the production of CP by industry is 61.6. At the same time, the remuneration in the first industry to ensure the output of the final product of the same industry is 25.3, and for the second – 36.3. But since there is an import of agricultural products, a certain amount of wages is imported accordingly. Therefore, as a result, the required amount of wages is reduced by the amount of its import (61.6–21.6 = 40).
The salary in the industry of the industry for the production of U1 is 25.3, but its import due to the negative U2 is -4.8. Therefore, the total need for remuneration is equal (25.3–4.8). A similar picture occurs in agriculture.