The logic of calculating total profit is similar to the logic of calculating total labor costs. Based on (6.5) we can write:
.
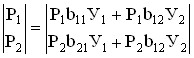Substituting the numerical values from Table 6.7 we get:
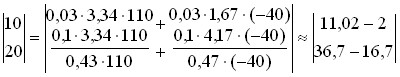
From the point of view of profit, the import of agricultural products is not as profitable as the import of industrial products, since it would be better to develop more profitable production (in this case, agricultural production) in your country.
Calculation of total value added by industry.
The value added in our simplified example consists of the amount of wages and profits. On the basis of the known coefficients of direct costs, it is easy to calculate the matrix of coefficients of total value added (see Table 6.7):
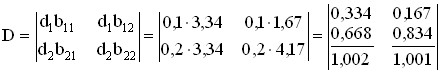
Let’s check the resulting matrix D:
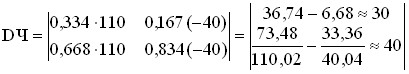
It turns out that 40 units of profit are imported at the expense of them.
port of agricultural products. From the point of view of unit value added, both industries turned out to be almost equivalent.
Calculation of total capital expenditures.
The technology of accounting for the total cost of capital for the output of the final product in industries is similar to the technology for accounting for total labor costs. Therefore, by analogy with (6.5), we write:
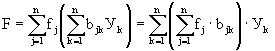, (6.8)
where F = F1 + F2 is the total volume of fixed production assets in the national economy, see Table. 6.7.
fj – coefficient of capital intensity of products of the j-th industry, Table. 6.8.
For our example, we have by analogy with (6.6) and (6.7):
F1 = f1⋅b11⋅U1 + f2 ⋅b21 ⋅U1 (6.9)
F2 = f1⋅b12⋅U2 + f2 ⋅b22 ⋅U2 (6.10)
F1 + F2 = = f1⋅b11⋅U1 + f2 ⋅b21 ⋅U1 + f1⋅b12⋅U2 + f2 ⋅b22 ⋅U2 =
= f1 (b11⋅U1 + b12 ⋅Y1) + f2 (b21⋅U2 + b22 ⋅U2)
F = (f1)’⋅V⋅Y
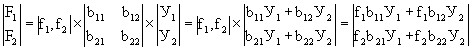
Substituting numeric values, we get:
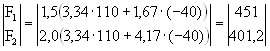
The result coincides with Table. 6.7. accurately rounded.
The matrix of total capital expenditure ratios consists of the following elements:
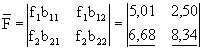
11,69 10,84
Thus, in terms of total capital expenditures, industry, as well as other factors, is more burdensome for the national economy than agricultural production (11.69>10.84).