The intersectoral balance is an economic and mathematical model of the reproduction process, which in a detailed form reflects the relationships on the production, distribution and accumulation of the social product in the context of the net branches of the national economy and in the unity of the material and material and value aspects of reproduction.
Since 1993, the Ministry of Statistics and Analysis of the Republic of Belarus has been annually developing intersectoral balances of production and distribution of products and services in the methodology of the System of National Accounts, which include 30-35 main branches of the national economy of the Republic, Fig. 6.1.
In the general scheme, the intersectoral balance is represented by four quadrants. In the first quadrant – indicators of material costs for production. The second quadrant presents indicators reflecting the final use of the products of industries (C – personal and public consumption, I – gross domestic investment, G – government consumption and ![]() – exports). In the third quadrant – indicators of value added (W – wages of employees, OP – gross profit and gross mixed income, TS – net taxes on production and imports) and imports (M).
– exports). In the third quadrant – indicators of value added (W – wages of employees, OP – gross profit and gross mixed income, TS – net taxes on production and imports) and imports (M).
Issue | |||||||||
Manufacturing Industries | Industries-consumers of intermediate Product | Finite product | Total: EaP For Use | ||||||
1 | 2 | … | n | With | I | G |
| ||
1 | a11 | a12 | … | a1n | C1 | I1 | G1 |
| X1 |
2 | a21 | a22 | … | a2n | C2 | I2 | G2 |
| X2 |
… | I intermediate product | II | … … | ||||||
Cost | … | ||||||||
n | a1n | an2 | … | ann | Cn | In | Gn |
| Hen |
Added value | W1 | W2 | … | Wn | I + II | ||||
OP1 | OP2 | III | OPn | = | |||||
TS1 | TS2 | … | TSn | ||||||
Import | M1 | M2 | … | Mn | |||||
Total: EaP by costs | X1 | X2 | … | Hen | I + III |
Rice. 6.1. Scheme of the intersectoral balance of production and distribution of products in the system of national accounts
Balance sheet data vertically reflect in each column the value composition of the output of economic sectors in the context of elements of intermediate consumption and value added. The sum of output and imports is the value of the available resources of industries. Horizontally, the directions of use of products and services of each industry are reflected: intermediate (production) consumption by industry and final use broken down by its components. For each sector of the economy, the total amount of resources used is equal to the total amount of available resources.
Direct cost coefficients are the unit costs of raw materials, materials, fuel and other items of labor of the supplying industries in value terms, for the production of 1 ruble. gross output of consumer industries. They are calculated by dividing the value of intermediate consumption by the total volume of production (gross output) of a given consumer industry.
Total cost ratios represent the costs of objects of labor in the value of the supply industries.
workers for the production of 1 ruble. final products of consumer industries. Their value takes into account not only direct, but also indirect costs that occur in other industries related to the production of the final product of the industry in question.
The mathematical model of the above scheme of intersectoral balance is the intersectoral static model of V. Leontiev (input – output model), the recording of which in vector-matrix form has the form:
X = AH + Y, (6.1)
where X is the vector of gross outputs of the industries covered;
A – matrix of direct cost coefficients;
Y is the vector of the final product of the industries covered.
For the case when the nomenclature of the intersectoral balance is represented by two industries, the model (1) has the form:
x1 = a11x1 + a12x2 + y1
x2 = a21x1 + a22x2 + y2, (6.2)
where x1, x2 are the gross outputs of industries;
a11, a12, a21, a22 – direct cost ratios,
1, 2 – volumes of the final product of the industries under consideration.
Let us explain that:
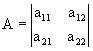 ,
,
and that:
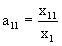 ;
; 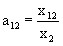 ;
; 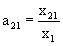
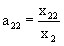
where x11, x12, x21 and x22 are the volumes of supplies of products of producing industries (first index) to consumer industries (second index) as objects of labor (raw materials, materials, components) and services.
The solution of the model (6.1) can be represented as:
X = (E – A)-1 Y (6.3)
where E is the unit matrix.
For two industries, equation (3) is:
x1 = v11u1 + v12u2
x2 = v21u1 + v22u2, (6.4)
where b11, b12, b21, b22 are the coefficients of total costs or costs of gross output of manufacturing industries per 1 ruble. the final product of consumer industries.
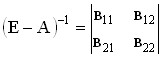 .
.
To consolidate the skills of calculation by modeling cross-industry relations, let’s consider a conditional example.