Сводка и группировка статистических данных

В результате статистического наблюдения получают «сырой» материал, записи об отдельных единицах наблюдения. Этот материал непригоден для непосредственного использования ни для практических целей, ни для целей научного анализа. Возникает необходимость в специальной обработке статистических данных, т.е. в сводке материалов наблюдения.

Сводка представляет собой комплекс последовательных действий по обобщению конкретных единичных данных, образующих совокупность в целях выявления типических черт и закономерностей, присущих изучаемому явлению в целом.

Задача сводки – охарактеризовать исследуемый предмет с помощью систем статистических показателей, выявить и измерить его существенные черты и особенности.

Статистическая сводка проводится по определенной программе. Разработать программу сводки – это, значит, определить, какие группы и подгруппы будут выделены в изучаемой совокупности, какие показатели в виде итогов, средних или относительных величин должны быть подсчитаны для выделенных групп и в целом по совокупности, в каких таблицах будет оформлен результат сводки.

При разработке программы определяют статистическое подлежащее и статистическое сказуемое. Подлежащее – это объект исследования, расчлененный на группы и подгруппы. Сказуемое – это статистические показатели, которые характеризуют подлежащее сводки.

По глубине обработки материала сводка бывает простой и сложной. Простой сводкой называются операции по подсчету общих итогов по совокупности. Сложная сводка представляет собой комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всему объекту и представление результатов группировки и сводки в виде статистических таблиц.

По форме обработки материала сводка может быть централизованной и децентрализованной. При централизованной сводке весь материал наблюдения сосредоточивается в одном центральном органе и там обрабатывается. При децентрализованной сводке материал наблюдения подвергается обработке на нескольких этапах (отчет производственного объединения района область итоги по области республика).

По технике выполнения сводка может быть ручной и механизированной (в настоящее время — доминирующая).

Группировки являются важнейшим статистическим методом обобщения данных, основой для правильного исчисления статистических показателей.

Расчленение совокупности на группы, однородные по какому-либо признаку, называется группировкой. Группировка является центральным моментом любой сводки. Именно благодаря группировкам материал наблюдения принимает систематизированный вид.

Впервые в статистике Д.П.Журавский уделил должное внимание методу группировок. Он считал основным методом анализа выделение и изучение «одновидных частей», категорий и групп.

Признаки, положенные в основу группировки, называют группировочными.

Всю совокупность признаков можно разделить на две группы: факторные и результативные. Взаимосвязь между ними проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает среднее значение результативного.

Группировочные признаки могут носить различный характер:

1) они могут иметь количественное выражение (возраст, заработная плата, объем выпущенной продукции). Эти признаки называются количественными, а группировки, построенные по этим признакам, называют вариационными рядами;

2) качественные признаки (социальное положение, профессия, пол, национальность). Группировки, построенные по этим признакам, называются атрибутивными рядами распределения;

3) территориальные признаки (группировка населения по областям, группировка предприятий по районам). Группировки, построенные по таким признакам, именуют географическими или территориальными рядами;

4) признак времени (группировка данных об объекте за ряд лет). Группировки, построенные по таким признакам, носят название рядов динамики.

Расчленяя совокупность на части и определяя численность по группам, при помощи группировок можно решить следующие задачи:

показать структуру совокупности; выделить основные типы и формы явления; выявить взаимосвязь между явлениями.

Группировки, при которых решается первая задача, называются структурными (табл.2). Структурной называется группировка, в которой происходит разделение совокупности на группы, характеризующие ее структуру по какому-либо варьирующему признаку. С помощью таких группировок могут изучаться: состав населения по полу, возрасту, месту проживания, состав предприятий по численности занятых, по стоимости основных производственных фондов и т.д.

Таблица 2

Распределение численности занятого населения по отраслям экономики (в процентах к итогу)

Группировки, при помощи которых решается вторая задача – выделение основных типов и форм явления, называются типологическими (табл.3). Типологическая группировка – это разделение исследуемой совокупности на качественно однородные группы.

Таблица 3

Жилищный фонд

(на конец года, миллионов квадратных метров общей площади)

Группировки, при помощи которых выявляется взаимосвязь между явлениями, называются аналитическими.

Особенности аналитических группировок следующие:

в основу группировки положен факторный признак; каждая выделенная группа характеризуется средними значения результативного признака.

Аналитические группировки позволяют изучить многообразие связей и зависимости между варьирующими признаками. Преимущество метода аналитических группировок перед другими методами анализа связи состоит в том, что он не требует соблюдения каких-либо условия для своего применения, кроме одного — качественной однородности исследуемой совокупности.

При построении таких группировок, из двух или более взаимосвязанных показателей один рассматривается как фактор (т.е. влияющий на другой), а второй – как результат влияния первого. Чтобы выявить зависимость между показателями, необходимо разгруппировать единицы совокупности по факторному признаку и для каждой выделенной группы рассчитать среднее значение результативного показателя и проследить за его изменениями (табл.4).

Таблица 4

Группировка предприятий по уровню производительности труда и себестоимости продукции

Статистическую группировку можно производить по одному или по нескольким признакам. Группировка по одному признаку называется простой, группировка по нескольким признакам – комбинационной (сложной).

Сложной называется группировка, в которой разделение совокупности на группы производится по двум и более признакам, взятым в сочетании.

Комбинационные группировки позволяют более глубоко анализировать развитие явлений, взаимосвязи и зависимости между ними. Комбинационной является группировка населения по полу и возрасту, группировка основных фондов по отраслям с подразделением каждой группы по натурально-вещественному составу (здания, сооружения и т.д.). Однако следует помнить, что чрезмерное дробление групп может только затруднить анализ материала. При правильном, научном применении комбинационных группировок они являются очень важным и эффективным средством обобщения и анализа статистических данных.

Особым видом группировок являются группировки-классификации. Примерами классификаций могут служить группировки предприятий по отраслям, основных фондов – по видам, затрат на производство продукции – по статьям и т.п. Для классификации характерно, что они производятся по наиболее существенным признакам, которыми определяются другие признаки и особенности изучаемого явления. Классификации имеют большое значение в статистике. При разработке классификации не только определяются признаки и интервалы классификации, но и четко устанавливается, какие единицы должны быть отнесены к каждой группе. Устойчивость признаков и интервалов, по которым производится классификация, обеспечивает возможность сопоставления данных за ряд лет не только по совокупности в целом, но и по отдельным ее группам.

Наиболее важными группировками классификации в отечественной статистике являются:

группировка предприятий по формам собственности; группировка (классификация) отраслей народного хозяйства; классификация отраслей промышленности; классификация основных фондов; классификация работников по категориям персонала (профессиям); классификация издержек; группировка предприятий по степени выполнения плана; группировка предприятий по размерам и т.д.

Классификации носят исторический характер: со временем появляются новые классификации или в ранее действовавшие классификации вносятся те или иные изменения.

Вторичная группировка – это перегруппировка ранее сгруппированных данных. Необходимость вторичной группировки возникает в двух случаях:

1) когда ранее произведенная группировка не удовлетворяет целям исследования в отношении числа групп;

2) для сравнения данных, относящихся к различным территориям и периодам времени, если первичная группировка была проведена по разным группировочным признакам или по разным интервалам.

Используют два способа вторичной группировки:

объединение первоначальных интервалов; выделение определенной доли единиц совокупности (долевая перегруппировка).

Имеются следующие данные о группировке предприятий по стоимости основных производственных фондов (ОПФ) (табл.5).

Таблица 5

Группировка предприятий по стоимости основных производственных фондов

Для целей анализа следует выделить следующие группы предприятий по стоимости основных производственных фондов (млн. руб.): до 20; 20-50; 50-100; 100-200; 200 и выше. Результат вторичной группировки приведен в табл.6.

Таблица 6

Группировка предприятий по стоимости основных производственных фондов

После определения группировочного признака следует решить вопрос о количестве групп, на которые следует разбить изучаемую совокупность. Число групп зависит от задач исследования и вида признака, положенного в основание группировки, численности совокупности, степени вариации признака.

Количественные значения признака, на основе которых исследуемые явления, лежащие в определенных границах, разбиваются на группы и называются в статистике интервалами. Смысл и значение интервалов в группировке зависят от ее конечной цели, от функций группировочного признака и взаимосвязи его с другими признаками, от задач исследования, от особенностей совокупности.

Каждый интервал имеет свою величину, верхнюю и нижнюю границы или хотя бы одну из них.

Нижней границей интервала называют наименьшее значение признака в интервале; верхней – наибольшее значение признака в нем.

Величина интервала – это разность между верхней и нижней границей интервала.

Интервалы группировок могут быть равные и неравные. Равные интервалы применяются там, где нужно показать, какие существуют количественные различия внутри групп одинакового качества, когда признак изменяется более или менее равномерно в ограниченных пределах. Равные интервалы устанавливаются механически, расчетным путем по следующей формуле:

, или же                                        (1)

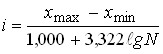(формула Стерджесса)                        (2)

где: , — максимальное и минимальное значение признака в совокупности;

n — число групп;

N — численность совокупности.

Формула Стерджесса имеет недостаток. Она дает хорошие результаты при большом объеме совокупности и если распределение единиц по группировочному признаку близко к нормальному.

Равные интервалы используются в тех случаях, когда соотношение максимального и минимального значений группировочного признака не превышает десятикратного значения.

В случае значительной вариации группировочного признака целесообразно применять кратные интервалы (удвоенные интервалы).

Полученную по формуле величину округляют. Она является шагом интервала. Существуют следующие правила определение шага интервала:

если величина интервала представляет собой величину, имеющую один знак до запятой ( например 7,35), то полученные значения целесообразно округлить до десятых и их использовать в качестве шага интервала (7,4); если величина интервала имеет две значащие цифры до запятой и несколько после запятой (15,671), то это значение нужно округлить до целого числа (16); если величина интервала представляет собой трех-, четырех — и так далее число, то эту величину необходимо округлить до ближайшего числа, кратного 100 или 50 (389 ≈ 400).

Пример.

Имеются данные о 10 предприятиях по выпуску продукции (млн. руб.): 16,2; 17,9; 15,4; 21,5; 18,1; 12,0; 14,9 13,8; 24,0 19,2. Произвести группировку предприятий по выпуску продукции, выделив 6 групп с равными интервалами.

Определим величину интервала:

i = = 2 млн. руб.

Для определения верхней границы первого интервала к прибавляем величину интервала (табл.7).

При группировке по количественному признаку границы интервалов могут быть обозначены по-разному. Если основанием группировки служит непрерывный признак, то одно и то же значение признака выступает и верхней, и нижней границами у двух симметричных интервалов. Если в основании группировки лежит дискретный признак, то нижняя граница i-го интервала равна верхней границе i-1 интервала, увеличенного на единицу.

Таблица 7

Группировка предприятий по выпуску продукции

В экономике чаще приходится применять неравные, прогрессивно увеличивающиеся интервалы. Применение неравных интервалов обусловлено тем, что с их помощью учитываются границы качественных переходов, т.е. выделяются группы качественно друг от друга обличающиеся.

Величина интервалов, изменяющихся в арифметической прогрессии, определяется                .

В геометрической прогрессии –        ,

где =const – число, которое будет положительным при прогрессивно возрастающих интервалах и отрицательным при прогрессивно убывающих интервалах;

=const – положительное число, которое при прогрессивно воз-растающих интервалах будет больше 1, а при прогрессивно убывающих – меньше 1.

В группировках, имеющих целью отобразить качественное своеобразие групп, применяются специализированные интервалы. В этом случае в каждой группе есть особое свое содержание, и граница интервала устанавливается там, где происходит переход от одного качества к другому (табл.8).

Таблица 8

Характеристика отношения мужского населения СНГ

к трудовой деятельности

Интервалы групп могут быть закрытыми, когда указаны нижняя и верхняя границы (табл.9).

Таблица 9

Суточный пробег автомобилей автотранспортного

предприятия

Интервалы групп могут быть открытыми, когда указана лишь одна из границ групп (см. табл. 8 – 70 лет и старше). Открытые интервалы применяются только для крайних групп. При группировке с неравными интервалами желательно образование групп с закрытыми интервалами, т.к. это способствует точности статистических вычислений. Ширина открытого интервала принимается равной ширине смежного с ним интервала.

Вариация признака в ряду может быть дискретной (прерывной) и непрерывной. При дискретной вариации значения вариантов отличаются друг от друга на вполне определенную величину и выражаются обычно целыми числами. При непрерывной вариации признака его величина может принимать любые значения в определенном интервале (см. табл.9).