As a result of solving the problems of optimal choice, it is possible to trace the relationship between changes in the price and income systems of a group of consumers, on the one hand, and the demand of this group for goods and services, on the other; and thus construct an optimal demand function.
In a fairly general form, optimal demand is expressed using functions of the form:
![]()
![]() .
.
In some cases, the functions of optimal demand have a particularly simple form. So, if the utility function has a logarithmic form, then the optimal demand is expressed by the formula:
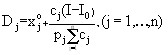
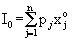 where .
where .
In the vast majority of cases, however, the specific form of the demand function is determined by statistical processing of the results of special observations of the income and expenditure of representatives of various social groups. As a result of the study of the demand function, some classification features of goods are usually established.
If the following condition is met for a certain product:
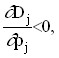
then the product is called normal, since the demand for it decreases as its price increases. However, there are goods for which the demand for which increases, despite the increase in price. This paradoxical situation arises when, with an increase in the price of an inefficient product (for example, potatoes), a group of low-income consumers simply cannot purchase a higher-calorie product (meat) and is forced to compensate for the lack of calories by increasing the purchase of potatoes.
Goods for which inequality occurs:
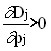 ,
,
are called anomalous or Giffin goods.
With a fixed income and for practical purposes, as a rule, demand functions of two types are used for normal goods:
1) Linear demand function
![]() ,
,
where a0 > 0, a1 > 0, the statistically estimated parameters of the model.
2) Power function of demand:
![]() .
.
In many applied studies, the elasticity coefficient plays a significant role.
A measure of the endogenous variable’s response to a change in an exogenous variable is called elasticity. However, this definition is too general. More specifically, elasticity can be defined as the limit of the relationship between the relative increment of the function y:
![]()
(dependent variable) and relative increment of the independent variable x:
![]() ,
,
when ![]() and is denoted by Ex(y).
and is denoted by Ex(y).
Thus, elasticity can be expressed by the formula:
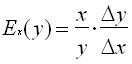 with
with ![]()
or in the continuous case:
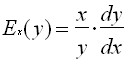 .
.
For practical reasons, elasticity is referred to as the percentage of growth of an independent variable. In this case, elasticity shows how much percent the endogenous variable Y rises or falls if the independent variable X changes by 1%.
A distinction is made between arc elasticity, that is, the average on some segment of the curve, and point elasticity – the value of the derivative at a given point. For the practical calculation of elasticity, the formula of the English mathematician and economist Roy Allen (1906 – 1983) is used. He suggested using the midpoint of the interval at which the change occurs as the denominator of the fraction. Then the following are calculated:
relative change in the endogenous variable
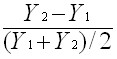 ;
;
relative change of exogenous variable
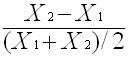 .
.
Then the ratio of the first to the second is calculated. It must be remembered that allen’s formula, although popular, is not the only possible one. However, it should not be applied to very wide intervals, as in this case it can be misleading.
To determine the elasticity of demand from price, you can use the formula:
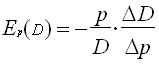 with
with ![]()
or
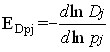 ,
,
The price elasticity coefficient of demand shows by how many percent demand will decrease (increase) if the price of goods increases (decreases) by 1%.
For a linear demand function, it is assumed that:
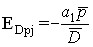 ,
,
where ![]() is the average value of the price,
is the average value of the price, ![]() is the average value of demand for the sample used.
is the average value of demand for the sample used.
Obviously, for the demand-level function:
![]() .
.
If the coefficient of elasticity is close to zero, then the demand for a product practically does not depend on its price. In this case, they say that demand is inelastic in price. This applies mainly to basic necessities. Demand is called normally elastic if the Edp ≈ 1, which is the case for durable goods. For luxury goods, usually Edp > 1, i.e. demand is super-elastic.
At constant prices, goods differ in the nature of the change in demand depending on the amount of income I. Commodity j is called a valuable (or higher-ranking good) if
 ,
,
i.e. the demand for it increases as it moves from less profitable groups of consumers to more profitable ones. For a low-value product, the opposite inequality occurs:
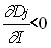 ,
,
which means displacing this product from the consumer set of a group of consumers as its profitability category increases.
On the basis of the above classification of goods into three groups, it is possible to present the change in demand depending on the increase in income using the graph presented in Fig. 5.16.
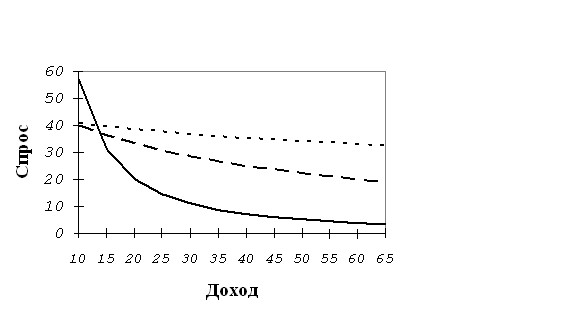 Rice. 5.16. Change in demand depending on income
Rice. 5.16. Change in demand depending on income
Here, the relative values of income are deferred along the horizontal axis (I), and the vertical share of expenses for these three groups of goods.
It is not difficult to see that the share of demand for essential goods falls from 70% (with low incomes) to 35% (with an income 10 times greater); the share of expenditures on goods of the second group is relatively stable (ranging from 20% to 27%) and the share of expenditures on luxury goods increases significantly (from 10% to 43%). To study the change in demand depending on the income of different consumer groups, two types of models are mainly used:
1) Models of power form (Engel functions):
![]() .
.
Here, the indicator γ makes sense of the coefficient of elasticity: because it shows how many percent the demand for the product will increase if the income increases by 1%. The coefficient of elasticity of demand from income is as follows:
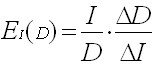 with
with ![]()
For basic necessities, the indicator γ < 1, i.e. with an increase in income, the additional costs for these goods of this category make up the entire decreasing share. For durable goods, the γ elasticity index is approximately 1, which means an approximate constancy of the share of expenditure on these items in additional income. For luxury goods, the elasticity index γ > 1. This means that with a significant increase in income, an increasing part of its growth is spent on goods of this group.
2) The idea of dividing the consumed goods and services into a number of different groups is further developed in the construction of the so-called Tornquist functions. For essential goods, this function is sought in the form of:
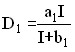 ,
,
where a1, b1 are the model parameters.
Note that with a very large income, conventionally represented as (I→∞) the value of demand ![]() , which expresses the fact of asymptotic saturation of the consumer with basic necessities.
, which expresses the fact of asymptotic saturation of the consumer with basic necessities.
Tornqvist’s demand function for durable goods reflects the fact that demand for these goods arises only from some (sufficiently high) level of income I2. The corresponding expression is of the form:
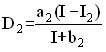 if I ≥ I2,
if I ≥ I2,
where a2, b2 are the model parameters,
![]() if I < I2.
if I < I2.
As can be seen, the demand for goods of this group also has an asymptotic tendency to saturation, since

For luxury goods, a formula is used in which there is no tendency to saturation, and demand begins with an even higher level of income I3:
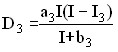 if I ≥ I3;
if I ≥ I3;
![]() if I < I3.
if I < I3.
It is easy to see that with sufficiently large income values I:
![]() .
.
This means that in this situation, almost all the increase in income is spent on luxury goods. A graphical representation of the Engel and Tornqvist functions is shown in Figure 5.17. and 5.18.
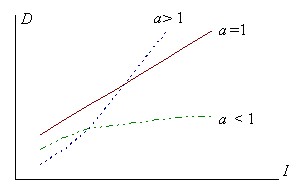
Fig. 5.17. Engel curves: growth in demand for different groups of goods depending on income
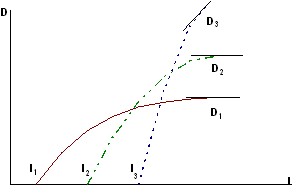
Rice. 5.18. Tornquist curves
Graphs of Tornquist functions for three product groups.